二つの文生成変形システム
Ti=(Gi,Gi,(Si,Di))(註1) (i=1,2)
が同型であることを,以下の条件を満たすことと定義する。
即ち,
Gi=(NVi,TVi,Pi,Si),
Si=(Gi,σi,Ri),
Gi=(NVi,TVi,Pi,Si),
Di=(VDi,PDi)
|
(i=1,2)
|
とするとき,
- G1とG2の間の(文生成システムの)同型f=(fN,fT)
- G1とG2の間の(文生成システムの)同型f=(fN,fT)
- 1対1対応 d:VD1─→VD2
で,つぎの条件を満たすものがとれる:
(1) fは,G1とG2の間の同型を導く。
(2) つぎの二つの図式はともに可換:
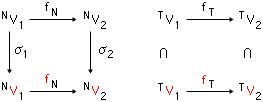
(3) fNとfNは,代入規則の間の1対1対応を導く;
(4) fとdは,1対1対応 PD1─→PD2 を導く(註2)
また,このときのf,f,dの組(f,f,d)を,T1のT2の上への同型と呼ぶ。
(註1) 文生成変形システム (G,H,(S,D))において,GとHは同値な文生成システムなので,Gは最初からHとしてとられていると考えてよい。したがって,G=Hとして一般性を失わない。
(註2) 即ち,Mi=TVi∪VDi(i=1,2)に対し,M1のM2の上への1対1対応hが,
h|TV1 =fT
h|TV1=fT
h|VD1 =d
|
で定義され,さらに
h*:M1*\{ε}─→M2*
が,つぎのように定義される:
h*(x1x2・・・・xn) =h(x1)h(x2)・・・・h(xn)
(x1,・・・・,xn∈M1)
このとき,h*|PD1がPD1とPD2の間の1対1対応になっていること。
|
