|
丂傢傟傢傟偼丆掕棟偺摫弌劅劅寢壥偐傜尒傞偲丆掕棟偺徹柧劅劅傪丆僥僋僗僩惗惉偲懆偊丆偙偺偲偒偺婯懃傪乬悇榑婯懃乭偲尒側偟偨丅偙偺傛偆側悇榑婯懃偼丆僥僋僗僩
偑惗惉偝傟傞偲偄偆帠幚偐傜 冇伣冋 傪寢榑偡傞傕偺偱側偗傟偽側傜側偄丅幚嵺偙傟偑乬墘銏掕棟乭偲偄偆儊僞(挻墇榑揑)掕棟偱弎傋傜傟偰偄傞偙偲偱偁傞丅偦偟偰偙偺偲偒丆堦斒壔婯懃 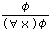 偼丆冇伣(佂倶)冇 傪掕棟偲掕傔傞傕偺偱側偗傟偽側傜側偄丅 丂偟偐偟偙傟偼捠梡偟側偄劅劅偙偺堄枴偱丆乬堦斒壔掕棟乭偼乬墘銏掕棟乭偲椉棫偟側偄丅 丂椺偊偽丆暥冇偲曄崁倶偵懳偟丆偮偓偺悇榑偑壜擻偵側偭偰 (佄倶)冇伣冇 偑掕棟偵側偭偰偟傑偆乮摿偵丆(佄倶)冇伣(佂倶)冇 偑掕棟偲側傞)丗 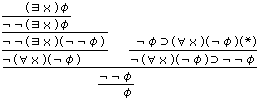
(*)丗堦斒壔婯懃偵墘銏掕棟傪揔梡偟偰摼傜傟傞掕棟丂 側偍丆傢傟傢傟偼 sen 喬 伿伿sen 傪曄宍婯懃偺昅摢偵埵抲晅偗傞丅 |