以下は定理シェマであり,≦が順序関係であることを示す:
(1) num≦num
(2) ((num≦num1)∧(num1≦num)) ⊃num=num1
(3) ((num≦num1)∧(num1≦num11)) ⊃num≦num11
また,(2)の証明では,証明すべき定理シェマとして以下のものが問題になる:
- ¬(num′=num)
- ¬(num+num1=num)
- ((trm=trm1)∧¬(trm=trm11)) ⊃¬(trm1=trm11)
- num+num11=num1 ⊃¬(num=num1)
- num<num1 ⊃¬(num=num1)
- ¬(num<num)
- num+num11=num1⊃num<num1
- (num<num1∧num1<num11)⊃num<num11
ここでは,つぎのことを確認する意味で,(2)の証明に至るこれらの定理シェマの証明をすべて示すことにする:
《手続きとして示せば極めて煩瑣なことを,手続きを殊更意識に上らせずにわれわれのカラダは実践できる》
-
(N1) より ¬(1′=1)。また,
| (a′)′=a′ | ←─ | num′=num1′
| | | ↓(N2)
| | a′=a | ←─ | num=num1
|
より,
よって,(N3) から所期の定理シェマを得る。
-
先ず,¬(1+b=1):
| | ε
| | | ↓(N1)
| | ¬(b′=1) | ←─ | ¬(num′=1)
| | | ↓(A1)
| | v¬(b+1=1) | ←─ | ¬(num+1=1)
| | ‖
| | ¬(b+1=1) | ←─ | ¬(num+num1=1)
| | | ↓§7.2.2,(2)
| | ¬(1+b=1) | ←─ | ¬(num1+num=1)
|
また,
| a′+b=a′ | ←─ | num+num1=num11
| | | ↓§7.2.2,(2)
| | b+a′=a′ | ←─ | num1+num=num11
| | ‖
| | b+a′=a′ | ←─ | num+num1′=num11
| | | ↓(A2)
| | (b+a)′=a′ | ←─ | (num+num1)′=num11
| | ‖
| | (b+a)′=a′ | ←─ | num′=num1′
| | | ↓(N2)
| | b+a=a | ←─ | num+num1=num11
| | | ↓(E2)
| | a+b=a | ←─ | num1+num=num11
|
よって,¬(a+b=a)⊃¬(a′+b=a′)。(N3)から,¬(a+b=a)。
-
項 f,g,h(記号‘f′,‘g′,‘h′ はメタ記号)に対し,以下の両方向の変形が成り立つ:
| (f=g)∧¬(f=h)⊃¬(g=h) | ←─ | sen∧sen1⊃sen11
| | | 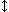 (C4) (C4)
| | ¬((f=g)⊃¬¬(f=h))⊃¬(g=h) | ←─ | ¬(sen⊃¬sen1)⊃sen11
| | ‖
| | ¬((f=g)⊃¬¬(f=h))⊃¬(g=h) | ←─ | ¬sen1⊃¬sen
| | | 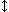 (T7),(C1) (T7),(C1)
| | (g=h)⊃((f=g)⊃¬¬(f=h)) | ←─ | sen⊃sen1
| | ‖
| | (g=h)⊃((f=g)⊃¬¬(f=h)) | ←─ | sen11⊃(sen1⊃¬¬sen)
| | | 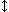 (C1) (C1)
| | (g=h)⊃((f=g)⊃(f=h)) | ←─ | sen11⊃(sen1⊃sen)
|
一方,(g=h)⊃((f=g)⊃(f=h)) は,(E3)より定理。
-
| a+c=b (仮定) | ←─ | sen
| | | ↓[2]
| | a+c=b | ←─ | sen
| | & | | &
| | ¬(a+c=a) | | ¬(num+num1=num)
| | ‖
| | a+c=b | ←─ | trm=trm1
| | & | | &
| | ¬(a+c=a) | | ¬(trm=trm11)
| | | ↓[3]
| | ¬(b=a) | ←─ | ¬(trm1=trm11)
| | ‖
| | ¬(b=a) | ←─ | ¬(trm=trm1)
| | | ↓[2]
| | ¬(a=b) | ←─ | ¬(trm1=trm)
|
-
数項 a,b と,これらの中に自由変項として現われない数変項 x に対し,
| a<b | ←─ | num<num1
| | | ↓(定義)
| | (∃x)(a+x=b) | ←─ | (∃num11)(num+num11=num1)
| | | ↓[4]
| | (∃x)(a+x=b) | ←─ | (∃num11)(num+num11=num1)
| | & | | &
| | (a+x=b)⊃¬(a=b) | | (num+num11=num1)⊃¬(num=num1)
| | | ↓(Q4)
| | (∃x)(a+x=b) | ←─ | (∃num11)(num+num11=num1)
| | & | | &
| (∃x)(a+x=b)
⊃(∃x)(¬(a=b)) | | (∃num11)(num+num11=num1)
⊃(∃num11)(¬(num=num1)) |
| | ↓(MP)
| | (∃x)(¬(a=b)) | ←─ | (∃num11)(¬(num=num1))
| | ‖
| | (∃x)(¬(a=b)) | ←─ | (∃trv)nf[tvr]
| | | ↓(Q3)
| | ¬(a=b) | ←─ | nf[tvr]
|
-
| | ε
| | | ↓(E1)
| | a=a | ←─ | trm=trm
| | ‖
| | a=a | ←─ | num=num1
| | | ↓[5]
| | ¬(a<a) | ←─ | ¬(num<num1)
|
-
数項 a,b,c と,これらの中に自由変項として現われない数変項 x に対し,
| a+c=b | ←─ | sen[trv↓trm]
| | | ↓(Q1)
| | (∃x)(a+x=b) | ←─ | (∃trv)sen
| | ‖
| | (∃x)(a+x=b) | ←─ | (∃num11)(num+num11=num1)
| | | ↓(定義)
| | a<b | ←─ | num<num1
|
-
数項 a,b,c と,これらの中に自由変項として現われない数変項 x,y に対し,
| a<b∧b<c | ←─ | num<num1∧sen
| | | ↓
| | (∃x)(a+x=b)∧b<c | ←─ | (∃num11)(num+num11=num1)∧sen
| | ‖
| | (∃x)(a+x=b)∧b<c | ←─ | sen∧num<num1
| | | ↓
| | (∃x)(a+x=b)∧(∃y)(b+y=c) | ←─ | sen∧(∃num11)(num+num11=num1)
| | ‖
| | (∃x)(a+x=b)∧(∃y)(b+y=c) | ←─ | (∃tvr)sen∧nf[tvr]
| | | ↓(Q2)
| | (∃x)(a+x=b∧(∃y)(b+y=c)) | ←─ | (∃tvr)(sen∧nf[tvr])
| | ‖
| | (∃x)(a+x=b∧(∃y)(b+y=c)) | ←─ | (∃tvr1)(nf[tvr]∧(∃tvr)sen)
| | | ↓(Q2)
| | (∃x)((∃y)(a+x=b∧b+y=c)) | ←─ | (∃tvr1)((∃tvr)(nf[tvr]∧sen))
| | ‖
| | (∃x)((∃y)(a+x=b∧b+y=c)) | ←─ | (∃tvr1)((∃tvr)(num=num1∧num1+num11=num111))
| | | ↓§7.2.2,(0),(Q4)
| | (∃x((∃y))((a+x)+y=c)) | ←─ | (∃tvr1)((∃tvr)(num+num11=num111))
| | ‖
| | (∃x)((∃y)((a+x)+y=c)) | ←─ | (∃tvr1)((∃tvr)((num+num1)+num11=num111))
| | | ↓(Q4)
| | (∃x)((∃y)(a+(x+y)=c)) | ←─ | (∃tvr1)((∃tvr)(num+(num1+num11)=num111))
| | ‖
| | (∃x)((∃y)(a+(x+y)=c)) | ←─ | (∃tvr1)((∃tvr)(num+num11=num1))
| | | ↓(Q4)
| | (∃x)((∃y)(a<c)) | ←─ | (∃tvr1)((∃tvr)num<num1)
| | ‖
| | (∃x)((∃y)(a<c)) | ←─ | (∃tvr1)((∃tvr)nf[tvr])
| | | ↓(Q3)
| | (∃x)(a<c) | ←─ | (∃tvr1)nf[tvr]
| | ‖
| | (∃x)(a<c) | ←─ | (∃tvr)nf[tvr]
| | | ↓(Q3)
| | a<c | ←─ | nf[tvr]
|
(2) の証明:
| a≦b∧b≦a | ←─ | num≦num1∧sen
| | | ↓(定義)
| | ((¬(a<b)⊃a=b)∧(b≦a) | ←─ | (¬(num<num1)⊃num=num1)∧sen
| | ‖
| | ((¬(a<b)⊃a=b)∧(b≦a) | ←─ | sen∧(num<num1)
| | | ↓(定義)
| | (¬(a<b)⊃a=b)∧(¬(b<a)⊃a=b) | ←─ | sen∧(¬(num<num1)⊃num=num1)
| | ‖
| | (¬(a<b)⊃a=b)∧(¬(b<a)⊃a=b) | ←─ | (sen⊃sen11)∧(sen1⊃sen11)
| | | ↓(T9)
| | (¬(a<b)∨¬(b<a))⊃a=b | ←─ | (sen∨sen1)⊃sen11
| | | ↓
| | ¬(a<b∧b<a)⊃a=b | ←─ | ¬(sen∧sen1)⊃sen11
| | ‖
| | ¬(a<b∧b<a)⊃a=b | ←─ | sen⊃sen1
| | | ↓
| | ¬(a=b)⊃(a<b∧b<a) | ←─ | ¬sen1⊃sen
| | | ↓[8]
| | ¬(a=b)⊃(a<b∧b<a) | ←─ | sen
| | & | | &
| | (a<b∧b<a)⊃(a<a) | | (num<num1∧num1<num11)⊃(num<num11)
| | ‖
| | ¬(a=b)⊃(a<b∧b<a) | ←─ | sen⊃sen1
| | & | | &
| | (a<b∧b<a)⊃(a<a) | | sen1⊃sen11
| | | ↓
| | ¬(a=b)⊃(a<a) | ←─ | sen⊃sen11
| | ‖
| | ¬(a=b)⊃(a<a) | ←─ | sen⊃sen1
| | | ↓
| | ¬(a<a)⊃a=b | ←─ | ¬sen1⊃¬sen
| | | ↓[6]
| | ¬(a<a)⊃a=b | ←─ | sen⊃sen1
| | & | | &
| | ¬(a<a) | | sen
| | | ↓
| | a=b | ←─ | sen1
|
|