数学教育学の最終ゴールは,授業の試案──指導案──である。いかなる学知的考察も,授業のための具体的試案として結実すべきものであり,この意味で,具体的な指導案こそが数学教育学の成果でなければならない。 この観点から数学教育学の現状を見ると,それはますます見通しの悪いものになりつつある。専門性志向の傾向と相俟って研究の射程が小さくなり,〈直接性〉が失われていく。 そこで,もう一つの種類の研究が必要になる。即ち,ゴール──指導案──を直接視野に置いて,そこへ大股に歩いていくといった態の研究である。 専門性という観点からは,この種の研究は"研究"とは見なされないだろう。しかし,数学教育の現場との対話性を第一義的に考えるならば,このような"研究"はなければならない。わたしは,このタイプの"研究"を"数学教育への素朴なアプローチ"と呼ぶことにしよう。 "素朴なアプローチ"は,乱暴な展開を余儀なくされるし,十分把握していない内容に言及したり,怪しい解釈を決断して行なうということもしなければならない。実際,大股に歩かねばゴールには到達しないのだ。 "素朴なアプローチ"は研究として認められるであろうか。わたしの考えは,"やってみなければわからない"である。 "素朴なアプローチ"に対する専門的立場からの批判は容易である。実際,"素朴なアプローチ"は専門的見地からの批判を呼び込み,それを自らの成長のための栄養にすることを見込んでいる。批判への防御が強迫になって瑣末にのめり込んでしまう専門的研究を,"素朴なアプローチ"は真似ない。 そこで,批判のルールが必要である。批判は,行論の粗さや偏り("独善性")──敢えて犯していること──を指摘して終わる非難であってはならない。《これこれの理由により,その大股はこのような大股にならねばならない》という形のものでなければならない。"素朴なアプローチ"の命はゴールへの〈直接性〉である。〈直接性〉が確保されてさえいれば,どのような破壊も許される。しかし,〈直接性〉を断ち切るような"指導"は困る。 本論は,わたしなりの"素朴なアプローチ"のための緒言である。わたしは,ここでは,大股の歩みをさらにはしょって途方もなく大股に歩くことになる。専門的立場から見て,わたしの物言いが全くの"シロート"のものであり,がまんできないものであることは,予想に難くない。しかし,これまで述べてきた意図を汲まれたい。 また,本論ではしばしば表象主義が──全く乱暴な形で──批判される。それは,わたしの考える大股の歩みに対し,表象主義的な概念装置が障害物として現われてくるからである。一般に,わたしの或る一歩は,或る障害物を随伴的に蹴飛ばしてしまう一歩になることがある。 0.2 本論の概要 第1章では,主題の導入と主題探究の第一次領域区分を行なう。この第一次領域化は,機能論,価値論,実践論の三領域の導入である。 第2章では,この三領域についての,言わば第一次オリエンテーションを行なう。機能論については,数学教育に対する〈関数〉の解釈を示す。特に,この関数の入出力になるものとして"テクスト"の概念を導入し,さらに存在者に対する一つの記述レベル──"テクスト内存在者"──として"傾向性"の概念を導入する。価値論については,価値に対するプラグマティックな立場を,わたしの採るものとして示す。実践論については,"投機性"の概念を,実践論の中心概念になるべきものとして導入する。 第3,4,5章は,それぞれ機能論,価値論,実践論の,言わば第二次オリエンテーションである。 第3章(機能論)では,いくつか概念装置──"言語ゲーム","道具−遊具","育てる/育つ","機能欠損","低迷−覚醒"──を導入する。 第4章(価値論)では,一般陶冶論に対するわたしの見解を示す。 第5章(実践論)では,実践論の領域区分を示す。はじめに,(1) テクストへの反応理論,(2) 指導案作成の実践論(狭義実践論),の区分を立てる。(1) についてはさらに,(1-1)"テクストへの反応"の理解図式,(1-2) コミュニケーション論,(1-3)〈内〉の扱い,という三つの主題を立てる。また,(2) については,(2-1) 教育の投機性,(2-2) 教材研究,(2-3) 指導案,(2-4) 各論,の四つの主題を立てる。 (1-1) については,わたしが伝来の意味中心主義的な図式と対峙/対決していかねばならないことを示す。(1-2) については,"コミュニケーション"に対するわたしの見解を示しつつ,わたしが対峙/対決しなければならなくなる図式として表象主義的図式について言及する。(1-3) については,数学教育学を実学と見るわたしの立場から,〈内〉が閑却して構わない問題機制であることを主張する。 (2-1) については,教育の投機性の二つの理由(構造)を示す。(2-2) については,"教材研究"のつぎの領域区分を示す:(2-2-1) ゴールとなる言語ゲームの同定(主題研究);(2-2-2) 学習者をこのゴールに到達させるために"授業"として逐次展開されるところのテクストの同定(指導法の研究)。(2-3) については,"指導案"におけるコミュニケーションの機能を確認する。 この"緒言"は,わたしが数学教育学のゴールと位置付けている"各論"に全く触れていない。したがって,この"緒言"で導入する枠組みを読者が全くの"空手形"と見なすとしても,それはもっともなことである。またそれ以前に,"意味不明"という形の批判が立ち得る。わたしは,各論をこの"緒言"に直ちに後続させ読者に是非を問う責務を負っている。(併せて,わたしの大股の歩みを精緻化する責務を負っている。) 1 問題設定 1.1 問題設定 教師がしていること,それは子どもを育てるということである。 "子ども"とは,教師が指導のゴールとして想定している(生活)主体Xに対する"前-X"の謂いである。そして前-Xと見なしている者に対しこれをXと見なし得る者に変えること,これが"育てる"の機能である。この機能が単に"変える"ではなく"育てる"と呼ばれなければならないのは,教師は《子どもが自ら変わるきっかけを子どもに与える》という形で子どもを変えるのみだからである(註)。 教師が相手にしているのは生体である。教育のゴールとなる主体Xもまた,生きている存在である。教育は屍体の改造ではない。教師がこの点において錯認することはあり得ないが,数学教育学者に対しては,このことはよくよく銘記するよう勧める価値がある。 ここで"生きている"とは,"常に既に逸脱している/差異を生み出している"の謂いである。 実際,"育てる"において,教師は
(2) 逸脱の奨励 教師は行儀を躾る一方で,学習者がその行儀を〈選ばれたもの〉として相対化し新しい可能性へ眼を向けるよう──そのような感性を自ら育むよう──導こうとする。要するに,教師は閉じた体系に子どもを導いてしまわないように心を配るのである。即ち,生きねばならぬ者を死なせないよう心を配るのである。 さて,以上の簡単な行論で,実はわたしの基本的な論点は尽くされたことになる。わたしの問題は,専らこの教師の実践である。彼が,何をしなければならないか,なぜそれをしなければならないか,そしてどのようにしたらそれができるか,この単純な問題がわたしの問題の全てである。──"わたしの問題"。わたしはこの言い回しを,本当は,"われわれの問題"に換えたく思う。しかし,この問題の設定では"教育は屍体の改造ではない"と言った所で一つの論点先取をしていると思うので(§1.2),以降も"わたしの問題"で通すとしよう。 さて,"数学教育とは何をすることか,それは何をしなければならないのか"という問いで問われているものは,数学教育の機能である。"なぜしなければならないのか"という問いで問われているものは,数学教育の意義あるいは価値である。そして,"どのようにしたらそれができるか"という問いで問われているものは,実践──数学教育の機能を実現することとしての実践──の仕方である。したがって,問題への探究はつぎのように領域化される:
数学教育価値論 数学教育実践論 (註) この認識については,わたしは中橋昭嗣(金沢市立金石町小),小山孝成(金沢市立新竪町小)の両氏に多くを負っている。(Cf.中橋・小山,"算数神経"を鋭くする指導,日数教第21回論文発表会発表要項,1988,pp.202-205.) 1.2 問題設定における論点先取について わたしは,"教育は屍体の改造ではない"──即ち,《教育を,屍体に関接する事態ではなく,生体に関接する事態として捉えなければならない》──は論点になるだろうと述べた。"そんなことは自明で,はじめから論点にならない"と言われるかも知れない。しかし,"つもりと実際にしていることは違う"ということを銘記してかからねばならない。"教育は屍体の改造ではない"のこころは,"数学教育学者は,生体を扱っているつもりで屍体を扱っていることがある"である。このように言えば,"そんなことは自明ではじめから論点にならない"という声は今度は少なくなり,論点とされるだろう。 "生体−屍体"の論点は,簡単な議論では収まらない。実際,これの主題化は,"形而上学,合理主義,機械論等の下の囚われと,そこからの脱出の可能性"という哲学上の大問題を主題化することにほぼ等しい。したがって,問題への探究に先立ってこの論点を予め鎮めておくというやり方は,論の構成のバランスの上で問題がある。そしてそもそも,読者を引き止めておくことが困難になるだろう。 しかしまた,この論点を見ないで済ますというやり方もとれない。"意味は差異において了解される"というのは本当である。わたしの探究は,この論点においてわたしが阻却しようとしている思考法との対照において,伝達可能となるだろう。 そこでわたしは,"生体−屍体"の論点を問題探究の行論の各所に分散させるとしよう。そしてこれらを,いわばスパイラルに鎮めていくとしよう。 2 機能論,価値論,実践論 2.1 数学教育機能論 2.1.1 数学教育に対する〈関数〉の解釈 数学教育機能論において,わたしは数学教育を〈機能=関数〉(function)として探究する。即ち,われわれの意識になる個々の数学教育的な事態を,関数として考察する。この解釈はつぎのことを可能にする:
《関数を下位の関数の合成の形に分節化する》というこの考え方でわたしが意図しているのは,つぎのことである:
2.1.2 〈質点−質量〉のアナロジー ここでわたしは,"質点の運動"をアナロジーとして考えている。力学は,物体xの運動を場──xはこれの構成因の一つである(註1))──の決定するものとして記述する。そしてこのとき,xは"質点−質量"に抽象される。われわれはこの図式から特に "xから運動が生じるわけではない,即ち,xの〈内〉が運動の原因なのではない" という含意を読むとしよう。"xの質量はxの〈内〉に遡行される(還元される)"という意味で,xの〈内〉は運動に効いている。しかし,xの〈内〉が運動の説明になるのではない。 "隠れているもの"が説明に効かないことを認識して,これにフタをする(フタが閉まったままにしておく),これが"質点−質量"の発想に対してわたしが読みたいと思う教訓である。そしてわたしはこの教訓を,数学教育に対する"関数"の解釈に適用しようと思うのだ。 アナロジーの読み換えはつぎのようになる:
関数のインプットは,一つのテクストである。テクストの中には,特に子どもがいる。子どもはそれの〈内〉──"隠れて見えないもの"──が問われないものとして扱われる(註3)。 さらに,このアナロジーにおける"質点"は,《運動の過程で旧い質点が消え新しい質点が替わって登場する》といったものでなければならない。そうでないと子どもの変容が扱えない。したがってアナロジーは物理学にのみとどまるわけにはいかない。それは化学を必要とする。即ち,《これまで焦点化していた質点が消え新しい質点が焦点化されるようになる》変化を扱う化け学。 そしてこのときにも,わたしは〈内〉を問わない。新しい質点を焦点化することだけを問題にする。この化学の主題は反応の中身──分析と統合──ではなく,反応のはじめと終わりを突き合せることである。即ち,これまでの焦点化していた質点と新しく焦点化することになった質点を,両者の質量において比較することである。 (註1) 場が在ってそこに存在者が在るというのではない。存在者の在ることが場である。即ち,〈存在〉が場である。 (註2) わたしは"テクスト"の語をこのように用いる。対象化において対象はコンテクストとともにある。"コンテクスト"とは"コン-テクスト(伴う-テクスト)"であり,"対象に伴っているテクスト"である。そして対象とそれに伴うテクストを合わせたものは,また一つのテクストである。 (註3) しかしこのことは関数のブラックボックス化を意味しない。われわれは関数について有意義なことを述べ得るだろう(質点の力学を想起せよ)。 2.1.3 傾向性の把捉 物体xの質量はxの〈内〉によって決まる。しかしこのことは,〈内〉によらねば質量を知り得ないということを意味するのではない。実際,xの質量はxの運動の様相から伺い知られる。 同様に,ある人の傾向性はその人の〈内〉──状態としての身体──により決まっているが,このことは,〈内〉によらねば傾向性を知り得ないことを意味するのではない。傾向性は,個々の状況においてその人がどのように振る舞うかを見ることで,知られるようになる。実際,われわれは人の傾向性を専らこのように判断してきた。逆に,われわれは〈内〉によって傾向性を計算する理論──即ち,《このような状況ではその人はこのような振る舞いをする》という予見を可能にするような〈内〉の理論──を持ち合わせていない。 人の傾向性を知る方法には,二種類ある。即ち,観察と実験である。ここで"実験"とは,その人に直接働きかけて反応を見ようとするものである。"対話"は"実験"の一つである──通常,このようには意識されていないが。 《人の傾向性の把捉は,専ら観察と実験の方法による》において第一次的な強調点となるのは,それの投機性ではない。《観察と実験が可能な方法になる》が強調点である。われわれのこの能力は,人知を超えている。(ここでの"人知"は,現時点で最高級のAIを作る能力という意味。) 2.1.4 "生体・屍体" 先の"生体−屍体"の対置(§1.1,§1.2)は,§2.1.2 で登場させたアナロジーを用いてつぎのように説明できる。 即ち,"生体"とは,場を伴い,場の中でのコミットメントにおいて意味付けられるような存在者の謂いであり,これに対し,"屍体"とは,場を伴わず,それ自身によって意味付けられる──例えば,それの〈内〉によって──ような存在者の謂いである。両者を区別するものは,"コミットメント"の概念の成立の有無である。 運動は,屍体の組織で説明されるものではない。この説明では,"力"が抜け落ちてしまう。──誤解のないようにしよう。"力"とは"場の力"のことである。われわれは〈内〉の力によって動いているのではなく,われわれを包摂している場の力(コミットメントの関係に生じる動因)で動いているのである。このように動いていることが"生きている"ということであり,われわれが屍体でないことの証拠である。 2.2 数学教育価値論 数学教育の利害関係は非常に入り組んでいる。社会の全体規模の動きが数学教育の現在・未来を定める。数学教育は理想で動けるのではない。数学教育のもたらすものが様々の形で現に使われているという現実──不均衡に,徹頭徹尾コンテクスト依存で使われているという現実──が最も重いのである。この現実には善し悪しのことばが入り込む隙はない。 特に,数学教育価値論は哲学的価値論ではない。それは社会学──しかも規範的ではなく記述的な研究領域の──に属する。 数学教育という現実がここに在る──これがわれわれの出発点である。ある意義を理由としてこの現実が在ると思ってはならない。意義は後追いの解釈である。そしてこの解釈は力にならない。また,力にしてもならない。(力は社会的な混乱を招く。) この現実に働きかけることとこれを仕切ろうとすることを,区別しよう。後者のことで焦ることはないだろう。無駄であるからというのではなく(もちろん無駄なのだが),してよいことではないからだ。 また,われわれは数学の"伝道師"にもなれない。数学は,"すばらしい"から使われているのではない。(不愉快な道具は色々あるではないか!)そして少なくとも,結果が出なくては"すばらしい"とはならない。特に,数学を際立った道具あるいは"遊び"用具として使うことがない人には,数学は永遠にすばらしくない。(われわれはこの事実に対して偽瞞的であってはならない。) ひとは"なぜ"を問いたがるが,現実は理由で動いているのではない。ただ動いているのだ。ただ動いているものに対し,理由づけを断念することはけしからんことだろうか?理念への収束を語ることは美しい行為だろうか? わたしは,デューイの言説に示されているようなプラグマティズム(デモクラシー)に即くのが最善であるように思われる。デューイであれば,教育の担当者や為政者の仕事は,眼前の交通に対し,これを目的論的に論ずることではないと言うだろう。交通の渋滞に用心し流れをよくすることに努めること,一旦渋滞が生じたときにはこれに適切に対処し流れを回復すること,これが彼らの努めである──それでよしとしなければならない,と言うだろう(註)。 (註) Cf. Dewey,J.,The public and its problems, Henry Holt & Co.,1927.[阿部斉(訳),現代政治の基礎:公衆とその諸問題,みすず書房,1969] 2.3 数学教育実践論 数学教育実践論は,関数としての数学教育を実現する方法を主題と定める論考である。注意しなければならないのは,関数は実現されるのであり,作られるのではない,ということである。実際,それは作り得ない。 われわれが作為するのは,一つのテクスト(§2.1.2,(註2))である。そしてうまくいけば,このテクストをインプットとし所期の事態をアウトプットするような関数が,自ずと形成される。(言うまでもなく,関数の形成は,所期の事態の現出を以って権利的に主張されるといったものである。) このように関数の実現は,手探りの実践である。それは〈賭け〉であり〈投機〉である。われわれは,"場の力"を利用するだけである。即ち,場の一部を作為し,或る所期の事態が場に現われることを期待するのみである。"教える"とは,このようなことである。 ただ,われわれは"教える"をこんなにも投機的なものとは感じていない。それは結構確実なものである。しかしこの確実性は,徹頭徹尾学習の成果,しかも系統的かつ個体的な学習の成果,である。 わたしはここで"系統的な学習の成果"を,特に強調するとしよう("個体的"の方は自明とされるだろうから)。 例えば,犬に教える場合,われわれは相応の教え方をする。この"相応"をわれわれはどこで知ったのか。それは,自ら発見したというよりも,伝来の知識として受け継いだものなのである。この知識のありがたさを,われわれは例えば"未知の生き物との遭遇"のところで味わうだろう──"宇宙人だろうか宇宙犬だろうか?"。そしてそのとき,"教える"(註)の本質が〈投機〉であることを嫌という程思い知るだろう。 誤解はないと思うが,"未知の生き物との遭遇"はSFとして言っているのではない。教師にとって授業はつねに"未知の生き物との遭遇"である。 (註) コミュニケーションは,コミュニケーション条件を逐次更新するという形で進行している。"条件更新"は"教える"に因っていることになるから,結局,コミュニケーションは"教える"として進行していることになる。 3 数学教育機能論 3.1 "言語ゲーム" 数学教育の〈機能=関数〉(function)は,子どもの変容──但し,変容前の子どもと変容後の子どもの対として──を用いて述べられる。そこで,変容に関してのそのときどきの子どもが何であるかを捉える概念が,必要になる。わたしは,"言語ゲーム"の概念を用いるとしよう。 "言語ゲーム"とは,言うまでもなく,ウィトゲンシュタインの謂う"言語ゲーム"である(註)。それは, 《根源的なもの──探究の出発点になるべく根源的なもの──は,哲学の伝来の概念装置ではなく,われわれが生きているというこの現実である》 ということを明確にするために導入された概念である。特に,《哲学者ならそこに規則の現前を読みたくなるようなわれわれの生活は,端的に"規則正しい"のであって,規則に従っているわけではない》ということが主張される。また"言語ゲーム"の概念には,伝来の哲学が形式や規則の網から漏れるとして排除してきたものを復権し,逆に形式や規則の方を阻却することが,含意されている。それは,意識の対象を境界がぼけているものとして引き受けようとする。それどころか,対象であるためには境界がぼけていなければならないと主張する。要するに,"言語ゲーム"は伝来の哲学を文字通り逆さにするのである。 おもしろいのは,このように逆さにしてみると,その方がむしろ自然に見えるということなのだ。翻って,逆立ちしていたのは伝来の哲学の方だったのではないかということになる。 さて,わたしが考えたのは,子どもの変容をこの"言語ゲーム"のことばを用いて述べるということであった。即ち,子どもの変容を,ある言語ゲームの主体から別の言語ゲームの主体への変容として捉えようというわけである。そしてそれは,数学教育の機能=関数を,ある言語ゲームの主体を別の言語ゲームの主体に変容させるものと捉える,ということである。この内容については,一般論として特に展開すべきものはない。わたしは各論においてこの方法を具体的に示すことになろう。 (註) Wittgenstein,L., Philosophical investigations, Basil Blackwell,1958. 3.2 用在論的数学論 3.2.1 用在論的数学論 数学教育の機能の考察においては,それ相応の用在(註1)論的な数学論が必要となる。ここでは,そのための簡単な枠組みを二,三導入しておこう。 先ず,数学の用在論的意義づけとして,道具と遊具の二つを考えよう。ここで"遊具"は苦しまぎれの造語だが,音楽とかコミックス等のわれわれにとっての意義を,金づちとか電話帳だとかの意義("道具")と対照させるためのものと理解されたい(註2)。 〈数学=道具/遊具〉を顕わす人々の実践は色々であり得るが,われわれはこのうち《道具/遊具を作る》と《道具/遊具を用いる》の二つのカテゴリーを問題にしよう。 〈作る〉と〈用いる〉に関しては,
(註1) 用在性(Zuhandenheit):用具的存在態様。 (註2) 誤解はないと思うが,"道具・遊具"はコンテクストに依存して決まってくる意義である。 3.2.2 数学の遊具的意義 理論家は,理論を生成するカラダをもっている。("理論を生成する規則をもっている"が普通の言い方になるが,ウィトゲンシュタインが示したように"規則"の概念は実は保持し得ない。)理論家は己れのカラダに従って理論を生成する。この意味で,自閉的に理論を生成できる。こうして作られた理論は,いつか誰かにとって道具になるかも知れない。この意味でそれは可能的道具であるが,しかしまた,この意味では何だって可能的道具になる。では何が理論の可能的道具としてのモラトリアムを許しているのか。 いくつかの場合が考えられる:
"つくった苦労を思えば,捨てる気がしない" "遊具として楽しめる" しかし,《数学=遊具》は,数学教育の主題として非常に困難なものである。われわれは数学で遊ぶことを数学教育的にどのように意義づけることができるであろうか。"遊び"はそれ自体が求められるものであって,ある目的に到達したり,見返りを得るために経なければならない過程ではない。したがって問題は,《"数学で遊ぶ"それ自体で完結するような数学教育的意義は何か?》である。 例えば,息抜きは学校生活で必要なものであり,このために"数学で遊ぶ"が採用されることはあり得る。しかし"息抜き"はここで考えようとしている意義ではない。何故なら,この意義は自己完結的ではなく,"つぎ・あと"を配慮しているからである。 わたしの見るところ,"数学で遊ぶ"の数学教育的意義は,"自己の内なる〈欠落〉の発見/確認"という枠組みで捉える以外にない。しかしそれはどのようになるか。わたしにはわからない。この主題についてはいまは保留するしかないし,特に,教材レベルで《数学=遊具》を積極的に立てることもできない。これはわたしの課題である(しかし,読者と共有したく思う課題である)。 3.3 ゴールとする言語ゲームのカテゴリー 教師は"教える"という行為で,子どもを或る言語ゲームの主体に育てあげることをしている。この理屈では,教師はその時々でゴールになっている言語ゲームがどのようなものであるかを自分なりに理解していることになる。しかし現実に必ずしもそうでないことは,改めて言うまでもない。用心しないと,テストである程度の点数をとることが,ゴールの言語ゲームになってしまう(註1)。 ゴールとなる言語ゲームのカテゴリーとして,いま,
(1-a) 〈数学=遊具〉で遊ぶ (2-a) 〈数学=道具〉を論ずる (2-a) 〈数学=遊具〉を論ずる (1) をもたらす数学教育の機能は,"体力づくり"である。特に (1-a) は,"職業訓練"──但し,就くかどうかわからない職業に向けてのの訓練──である。これに対し,(2) をもたらす数学教育の機能は,メタ-労働者/遊戯者としての"思想家"の育成ということになる。 (1) をもたらす機能は,子どもを型にはめることを目的とするものであり,(2) をもたらす機能は,型から逸脱させることを目的とするものである。このような意義において,それらは互いに補完する関係にある──但し,微妙でスリリングな対立関係にある補完関係。それは言わば,束縛対自由,あるいは参入対逸脱,あるいはファッショ対アナーキーの対立であるが,一般に教育はこの対立のバランスの上に成立する。 しかし,自由−逸脱−アナーキーの路線(註2)は,これまでの数学教育において殆ど主題にならなかったと言える。この主題は,取り上げなかったのではなく,単に気づかれなかったのかも知れない。しかしいずれにせよ,取り上げられてこなかったということは,数学を警戒する──即ち,数学がヨーロッパの独特な思考様式の一つの現われであることを銘記し,このようなものとして相対化しつつ,警戒して対峙する──必要を認めていないということになる。 わたしは,この主題は数学教育で取り上げられるべきであると思う。そうでなければ教育としてのバランスを失することになる。わたしとしては,各論的にこの主題の実現を試行するとしよう。 (註1) テストにパスする言語ゲームをゴールと定めてよい場合があるかも知れない。しかしいまは,これは論外としておこう。 (註2) 強調点は,"開いている"ではなく,"現前しているものからの逸脱"である。 3.4 〈数学=道具〉を使う言語ゲーム 〈数学=道具〉を使う言語ゲーム──"数学の応用"──にア・プリオリな要素はない。それは未知を既知にするように学習するしかない。 例えば,赤インク 1cc を水 10cc で薄めたときの色と赤インク 2cc を水 20cc で薄めたときの色が同じになることを予知するために数学が応用できる。しかし,この場合に数学がしかるべく応用できるという事実は,純粋に経験的である。数学が応用できるためには,応用の対象になる素材について実に多くのことを知っていなければならない(註)。しかし一方,われわれは長い学習経験を通じて,この実に多くの知識を〈当たり前〉にしてきている。"当たり前"とは意識にさえ上らないということである。 そこで,教師には自分の〈当たり前〉が見えない。そして,教師の〈当たり前〉が当たり前になっていない子どもが,それに躓く。 (註) J.Piaget の構造主義的な認知発達観は,このことの閑却の故に誤まっている。 3.5 "育てる/育つ" 教育の機能は,学習主体を或る言語ゲームの主体へと育てることであるが,このとき,個々の指導局面(テクスト)は,学習主体が言語ゲームの主体へと成長するための"食物"として意義づけられる(註)。 ここで"食物"という比喩を用いるのは,《指導は契機以上のものではない》ということをはっきりさせるためである。またこの比喩は,指導が"添加する(欠落に対してこれを補綴する)"ではないことをはっきりさせる。実際,"食物Xを食することで行為Yができるカラダになる"と言うとき,X=Yではない。(食べた肉が自分の肉として現われるわけではない。) 教師にできることは,学習主体に食物Xを食べさせることのみである。学習主体がXを食べることによって行為Yをするカラダになるプロセス("化学反応")に対しては,教師は関与するものではない。これが"育てる/育つ"ということである。 (註) 但し,"食物"については,"成長をもたらす"の意義の以前に,"エネルギーをもたらす"の意義があることを忘れてはならない。 3.6 機能欠損の教育 教育=機能の図式:
《学習主体に食物?を食させ,行為Yができるカラダに成長させる》 ひとはしばしば"X=Y"("食べた肉が直接自分の肉として現われる")と考えてしまうが,この錯認の導く教育では,論理上,少なくともXかYの一方が欠損していることになる(註)。 教育の機能欠損は,しかし,"X=Y"とする錯認を専ら原因とするのではない。実際,教育事業は準備万端整ったところから始めているわけではない。それはつねに試行している。機能の欠損の解消を自らに課して,歩んでいるのである。 しかし例えば,"数学教育の現代化"は,"X=Y"の錯認に因る教育の機能欠損から失敗したと言える。実際,《現代数学を食わせることで現代数学が身につく》と単純に考えられたのだ。つぎのことが必要であった。即ち,指導を固定するとき,それがどのようなゴール=言語ゲームを見込んでいるかを明確に把握していること。また,ゴール=言語ゲームを固定するとき,指導を確実な"食物"として実現していること。"現代化"にはこれがなかった。したがって,"現代化"については,失敗したというよりそもそも遂行されなかったと言う方が適切かも知れない。 "遂行されなかった"という見方を入れるとき,"小学算数","中学数学","高校数学","大学数学"のようなことばも安直には使えなくなる。実際,それらは遂行されているのか? 即ち,図式:
先に述べたように,教育の事業は教育の試行であり,X,Yは多くの場合埋められてはいない。しかし,X,Yが公けに埋められている状態がよいというわけではない。このことは強調しておく価値がある。自由−逸脱−アナーキーの路線(§3.2)は,教育にタッチする者の集団についても貫徹されていなければならない。 機能欠損の教育がそこにあるということが問題なのではない(それはつねにある)。"機能欠損"がはじめから意識に上っていないこと,それがあるとすれば問題なのだ。言うまでもなく,われわれは教育の機能欠損の解消をつねに志向する者でなければならない。 (註) 《X=Y》の錯認のうちに,"X=Y=教科書"がある。教科書そのものはもともと完結した食物として作られているわけではなく(勿論,しようとしてもできない),また,教科書が"読める"ことがゴールとなるわけでもない。〈教育=関数〉にインプットされるテクストの一部に教科書が組み込まれる。教科書はあくまでも〈テクスト=食物〉の一環である。 3.7 低迷と覚醒 わたしは,学習を〈低迷−覚醒〉の図式で捉えるとしよう。 言語ゲーム主体は,まさに覚醒("悟り")という様相で誕生する。実際,言語ゲーム主体の誕生は,一つの身体が出来上がること──この一部として,一つの脳(状態)が出来上がること──であり,それは成長のカタストロフィー点である。これの特異性を表現する言葉として,わたしは"覚醒"より適切な言葉を差し当たり見出せない。 〈誕生以前〉は誕生のための必要条件であるが,これの機能的様相は〈できる〉に対する〈できない〉である。即ち,それは機能的にはゼロの状態である。わたしはこの〈誕生以前〉を"低迷"と表現する。但し,"低迷"は,下位の〈低迷−覚醒〉の連鎖へとさらに分析されることに対し開いている。 〈教育=関数〉との関連で言うと,〈低迷−覚醒〉は〈教育=関数〉の様相を述べる概念装置の一つとして導入されていることになる。即ち,〈教育=関数〉のインプットの中にあった子どもを関数の中でトレースしようとする場合,〈低迷−覚醒〉は子どもの変容過程を捉える第一次的な枠組み──最も粗い枠組み──になる。 4 数学教育価値論 4.1 一般陶冶論 4.1.1 "一般陶冶" 数学教育価値論の伝統的な形態の一つに一般陶冶論がある。しかしまた,数学教育の価値展望の不能(§2.2)にあってわれわれがなおも数学教育の一般的価値を積極的に語ろうとするならば,一般陶冶の価値論的主題化しかあるまい。実際,価値展望の不能をものともしない──即ち,価値展望の不能を何でもないものとする──数学教育価値論は,"何が来ようと大丈夫"を何らかの仕方で保証するものとして成立するのみである。伝来の数学教育論は,これを"一般的能力の陶冶"という形で引き受けようとした。 一般陶冶論は,教育価値論である。それは,
(1) については,議論の余地はない。一つを教えることは無限に多くのものを教えたことになる。このことは,われわれにとって経験的に自明である。 すると (2) の考え方はどういうことになるのか。二つの場合が考えられる。即ち,(1) の意味での一般陶冶が信じられていないか,(1) の意味での一般陶冶に満足していないかである。常識的には後者であるが,今日の一般陶冶論──表象主義的な一般陶冶論──は,既にこの論点の段階で際どい位置に自らを追い込んでいる。即ち,後述するように,理論に自縛されて (1) を信じられない格好に自らをなしている。 4.1.2 二つのモデル 一般陶冶論は"転移"を論拠とする。そして,自らの論拠であるこの"転移"を捉えようと努めてきた。 今日の一般陶冶論は問題解決論(ストラティジー論)の姿で,表象主義に立っている。しかし表象主義で"転移"を捉えようとする試みには,はじめから構造的な無理がある。表象主義は,"転移"と相性が悪い。 即ち,表象はぼやけてくれないのだ。そしてこのような表象でつくられた構造── 一つの能力──も,当然ぼやけてはくれない。表象主義の概念装置では,転移のような柔らかい出来事を作り出せない。それは,言い換えれば,フォン・ノイマン型コンピュータのアーキテクチャの上では柔らかさを作り出せないということだ。 ここで,コネクショニスト・モデル(PDPモデル)(註1)の登場となる。コネクショニスト・モデルは"柔らかさ"そして"転移"と相性がよい。 フォン・ノイマン型のアーキテクチャは,決定論で作られている。特にそれは,入力をコントロールしている。即ち,入力を有意味とする規格が予め定められていて,この規格から外れる入力を,表向き受け入れつつも,内部で無効なルートに流して消尽してしまう。言い換えると,圧倒的多数の入力が,《機械の状態を変えない,出力も産まない》入力だということである。これがフォン・ノイマン型の── 一般に,表象主義の──固さだ。 これに対しコネクショニスト・モデルは,入力をコントロールしない(できない)。すべての入力が同格で実質的な入力になる。そして,うまく育てれば,似た入力に対して似た出力を行なうようになる。これが,コネクショニスト・モデルの柔らかさだ。 表象主義に立って転移を説明するのが困難なのは,表象主義が決定論だからである。決定論では"転移"もプログラムされていなければならない理屈だが,未知の入力に対して開いていることをプログラムすることは,決定論としてできない相談なのだ。 これに対しコネクショニスト・モデルでは,〈似た入力に対して似た出力をするように成長していく存在者〉を実現できる。コネクショニズムのこれまでの成果がどれほどのものかということは,ここでは問題ではない。重要なことは,それが確実に〈知能〉理解の現実的な方向を指し示しているということなのである。(しかも,コネクショニスト・モデルが〈知能〉理解の現実的な方向を指し示すのは,"転移"の主題に限らない。) 但し,誤解がないようにしておかねばならない。コネクショニスト・モデルの現実性は,人間の真似ができるということにあるのではない。人間の原理を自ら示しているということにある。 "似た入力に対して似た出力"という言い方は,実はミス・リーディングである。コネクショニスト・モデルは"似た入力に対して似た出力"をするのではなく,自らの入力−出力の対応で"似ている"を定義するのである。"似ている"はカラダから決まる。コネクショニスト・モデルはこの人間の原理を自ら示す。 表象主義は,これとは逆方向に考える。即ち,"似ている"には根拠として形式が立たねばならない;カラダはこの形式に反応する;形式および形式へのカラダの反応に関して"似ている"を言うことができる──それはロジックとしてア・プリオリである;互いに似た形式に対しカラダは互いに似た反応をする。 整理しよう。表象主義は所謂ロゴス中心の立場に立ち,ロゴスの方からカラダを──ロゴスに従うカラダとして──見ようとする。コネクショニズムは,カラダ中心の立場に立ち,カラダから定義されてくる世界を見ようとする(註2)。 (註1) Cf. Rumelhart,D.E.,McClelland,J.L.,and the PDP Research Group, Parallel distributed processing: explorations in the microstructure of cognition, vol.1,2, 1986.[甘利俊一(監訳),PDPモデル:認知科学とニューロン回路網の探索,産業図書,1989.] (註2) コネクショニストがコネクショニズムをこのように捉えているというのでない。あくまでもわたしがコネクショニズムに見ようと思う意義である。 4.1.3 一般陶冶の不透明さ コネクショニスト・モデルに即けば,"教える"はつねに一般陶冶である(勿論,程度問題として)。しかしその一般陶冶は計算が立たない。一般に,コネクショニスト・モデルの〈成長〉は計算が立たないのである。したがって特に,《われわれは"一般陶冶"を経験的に知っているが,それ以外の形では知りようがない》ということになる。 一般陶冶を直接射程におく指導を考える向きがあるが,われわれは"一般陶冶"のはかり難さを十分認識すべきであろう。そもそも,われわれは現行の指導の一般陶冶としての射程さえ知ってはいない。 4.1.4 一般陶冶論としてのストラティジー論の特異性 今日の一般陶冶論は,問題解決論──特にストラティジー論──である。そしてそれは,表象主義に立つ一般陶冶論である。 既に述べたように,表象主義は,常識的な一般陶冶──"一つを教えることが無限に多くのものを教えたことになる"──を理論化できない。したがって表象主義者は,自分の立場を貫徹するとき,"常識的な一般陶冶を自分は信じない"と言わねばならなくなる。 この帰結は恐らく彼らにとっても不本意であろう。しかしこの"不本意"は,己れの理論の解体を表現するものに他ならない。表象主義者は自らの主義によって自己解体する。 しかし"不本意"の後に来るこの結論──"自己解体"──は,"不愉快"に違いない。したがって,表象主義者に対してはむしろ,常識的な一般陶冶を信じない方向に進んでいると見た方が失礼がない。特に,表象主義者たるストラティジー論者の場合,《彼らは,単に常識的な一般陶冶を物足りないものと感じて"ストラティジー"の概念を導入したのではなく,この概念の導入で常識的な一般陶冶をも説明することを目論んでいる》と見なされるべきである。ストラティジー論者は,"転移"一般を"ストラティジー"の言葉で理解しようとする。それは既に述べたように,"似ている"の根拠を立てる考え方であり,そしてその根拠として形式を立てる考え方である。この考え方が,ストラティジー論を特異な──即ち,西欧的な考え方に染まっていないわれわれに"特異"と感じさせる── 一般陶冶論にしている。 5 数学教育実践論 5.1 数学教育実践論の二分法 数学教育実践論の問題領域は,大きく,
(2) この理論を援用しつつ行なう指導案作成の実践論(狭義実践論) (1) は伝統的に"教授/学習"理論と呼ばれてきたものに対応するが,"教授","学習"という特権的なスタンスが存在するわけではないということを強調する目的で,"テクストへの反応理論"という言い回しを用いることにする。 "教える"とはただ単に,一つの〈他者への働きかけ〉である。"教える/学ぶ"とは,生活形態の一つである。教師は,学習者のためによかれとして一つのテクストを作為する。これが"教える"である。"教える"とは"何かを教える"ではない。なおのこと"真実を教える"ではない。 "本当か嘘か"という問題の立て方をすれば,教師は学習者に"嘘"を教えている。どういうことか?──つまりこういうことである:本当も嘘もないところで教師は《本当を教える》というスタンスをとる;このことにおいて教師は"嘘"をついている。 教師は自らが作為したテクストに直ちに裏切られる。(この感覚を持たない教師は単に鈍感ということだ。)教師がテクストを作為することそれ自体がテクストになる。教師と学習者は個々にこのテクストに反応する。そしてこの反応がまた新たにテクストを創出し,随伴的に先行テクストを消し去る。 (註) §2.1.2,(註2)。 5.2 テクストへの反応理論の問題領域 テクストへの反応理論の問題領域としてわたしが考えるのは,つぎのものである:
(2) コミュニケーション論 (3) 〈内〉の扱い (1) の主題が課せられるのは,テクストに対する意味中心主義とでも呼び得るような伝統があり,これの中に投げ込まれているという状態からわれわれが出発することになるからである。われわれは,この伝統に対して自分なりの対峙の仕方をつくらねばならない。 (2)"コミュニケーション論"は,"テクストへの反応"の中から"コミュニケーション"を焦点化し主題化するものである。これは,テクスト一般のうち,"働きかける主体"が存在しているテクストを取り上げる。 (3) の問題は (1) と一部重なるものであり,人の運動の説明あるいは記述という主題において人の〈内〉をどのように扱うかという問題である。西欧の伝統的発想は,一貫して〈内〉にこだわってきた。近くには,"認知科学"という現象がある。数学教育学でも,認知科学の流行に力を得て,てらいなく〈内〉を議論できるようになっている。(3) の主題は,このような現実を背景としている。 5.3 指導案作成の実践論 指導案作成の実践論(狭義実践論)の問題領域を,わたしはつぎのように考えることにする:
(2) 教材研究 (3) 指導案 (4) 各論 (1) の主題は,投機性を教育の本質として捉えることである。投機性は,教育に関わる否定性として問題になるのではない。われわれが見なければならないのは,逆にこれの肯定性である。投機性を本質としていることで,教育は自閉しない/できない。教育をつねにそれ自身から逸脱させ,可能性に開かせる契機,それが投機性である。 (2) の主題はありふれたものであるが,しかし奥行きの深い主題である。この行論が深いものになるか薄っぺらなものになるかは,ひとえに"教材"という概念の把握に掛かっている。意味中心主義的な"教具論"の形でこの主題が貫徹されると考える人の行論は,薄っぺらなものになろう。逆に,"テクスト論"として混沌に直接対峙しようとする人の行論は,極めて深いものになろう。 (3)"指導案"の主題もありふれたものであるが,ここでわたしが特に強調したいのは,指導案は読者を教育する機能を持たねばならないということである。指導案はそれを"指導案"として読める人を読者に想定して作成される。そして,"指導案"が読めることは,一定の学習の成果としての能力である。したがって,"指導案"を自己完結的(self-consistent)なものに近づけようとするときの指導案作成のスタンスは,"読者に教える"──"作成者であるわたしを理解させる"──である。こういったわけで,指導案の作成は,一つの体系を作ることと等しく,そこには通常思われているよりはるかに多くのことが書かれねばならないのである。 最後の (4)"各論"は,個々の指導内容(数学的主題)に各論的に応ずる実践論である。そしてこれが,数学教育学の最終ゴールである。 5.4 脱-意味中心主義 5.4.1 意味中心主義 テクストに反応することを,"テクストの意味に反応する"というように解釈しようとする,根強い伝統がある。それはもともと西欧のものでありわれわれのものではないが,先人がせっせと輸入に努めたおかげで,いまやわれわれにとっても自然なオリエンテーションになってしまった。ここで"自然な"とは,意識に上ることさえないということである。 このオリエンテーションを図式化すれば, 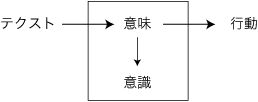
プラトンに発すると見なされているこの伝統は,《対象がその都度異なる双貌で現われるにも拘らず,われわれがそれを同一のものと認めるのは何故であろうか?》という問いに一貫してこだわるものである(註)。 そしてこの伝統は,〈本質〉とか〈真理〉とかを以ってこの問いに答えようとすることにおいて,本質主義,真理主義である。 〈本質〉は色々な言い回しの下で色々に考察されてきた。プラトンは,それを〈イデア〉としてわれわれの〈外〉に理由を求めた。しかし,デカルトのコギト以来,〈本質〉をわれわれの〈内〉によって説明することが趨勢になった。現象学(フッサール)はこの本流の中に位置づく。 テクストに対してこれの意味を見ようとする発想は,この伝統下のものである。テクストは不安を喚起するものであり,テクストを意味に還元することで安心が得られる。しかも,意味に対してテクストはかりそめのものでしかない。したがってこの伝統は,意味中心主義とも呼び得る。 〈意味〉を人の〈内〉に実現するために,"(内的)表象"が発想された。《一つの対象がそれの多様な見かけにも拘らずつねに同一のものと認識されるのは,つねに同一の表象がこれに対応させられるからだ》というのがこの場合の論法になる。また,先の図式が 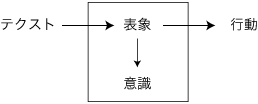
(註) これは認識論であるが,行為を閑却しているわけではない。行為の適切さを認識の正しさに還元するので,認識のみが問題になる。 5.4.2 反-意味中心主義 意味中心主義は,虚心坦懐にこれを省みるならば,極めて特異な思想である。なぜ西欧の哲学者はそんなにも"対象の同一性",即ち"X=X"にこだわったのだろうか(註)。なぜわれわれの生活の根底に"X=X"がなければならないと思うようになったのだろうか。 彼らはたかだか自分が生きた数十年の間に得た言葉で,生命の数十億か数百億年の歴史の到達点を理解しようとしたのだ。 そして特に,表象主義。──伝来の哲学は,人の傾向性を"心"と捉え,その機制を"(内的)表象"のアイデアに拠って理解しようと努めてきた。そしていま,表象主義は哲学者の専売ではない。表象主義は,心理学に,認知科学に,そして数学教育学にも,浸透している。 表象主義者は,表象による解釈の枠組みから漏れるものを容赦なく捨ててきた。捨てることを,"簡単なところから始める"という言い回しで合理化し,捨てたものの回収を見込んでいることをほのめかした。彼らはつぎのことに気づかなかった──また,気づいていたとしたら,とぼけていたことになる。即ち,"簡単なところから始める"と考えたとき,既に構築してしまっているのだということ。実際,彼らはつぎのことを前提していることになる:
却ってこう考える方が自然ではないか。即ち,"数十億/数百億年の歴史の到達点の奥深さの前には,人知(ことば)などものの数ではない;このような人知(ことば)に引き寄せて奥行きを理解することは,定めし錯誤である;あなたは〈表象〉を導入しないと理屈が立たないと言う;しかし理屈を通すよりも理屈を捨ててしまう方が賢明なのではないか;テクストにまるまんま──即ち,無媒介的に──反応できること,それはありそうなことだ;あなたは腑におちないと言うだろうか;しかし腑におちるものこそ錯誤なのではないか",と。 このような物言いは無責任で問題回避に聞こえるだろうか。しかし"問題回避"を言うその"問題"がそもそも違うのではないか。そのような問題に対して連帯責任を要求するのは間違っているのではないか。 "問題が違う"という論点を専ら焦点化する議論は読者を引きつけないだろうから,この論点への深入りは自重すべきであろう。しかしまた,"その問題は違うのではないか"という疑念のあり得ることを看過させるわけにもいかない。したがって,論点を忘却させないという意図の限りで,わたしはこの論点を以降も色々な形で適宜蒸し返すことになろう。 (註) もちろん正しくは,この問題にこだわる人種が"哲学者"と呼ばれる,ということである。 5.4.3 反-意味中心主義の図式 わたしは,意味中心主義の図式に対し,図式: 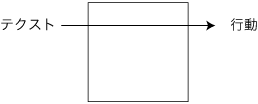
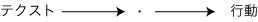
こころは,
"行動"に解消される"意識"には,意味-の-意識もある。但し,意識される〈意味〉というものがこの意識以前にあるのではない。あくまでも"意味を意識する"と表現したくなるような意識があるということである。 わたしの第一の図式はすべてをブラックボックスにしているような見掛けを呈しているが,主旨は,〈内〉を抹消する──特に,媒介項としての"表象"を錯誤として抹消する──ことにある(よって第二の図式の方がよい)。そこで特に, この帰結がきつ過ぎると感じられるとしたら,それはとりもなおさず,意味中心主義がきつ過ぎるということなのだ。(意味中心主義は一つの根本的な原理であり,そのためにこれがコケたときの波及効果は甚大なものにならざるを得ない。)このことはよくよく理解し,銘記しよう。反-Xがきつくなるのは,Xがそもそもきついからなのである。 (註) "言葉を口に出さないで言うことと,口に出して言うことの間に本質的な違いはない"──これと同じ主旨で"意識"は"行動"から区別されるものではない。 5.4.4 コネクショニスト・モデルの意義 伝来の〈人間=機械〉は専ら〈人間=表象主義的機械〉であった。したがって,反表象主義的機械としてのコネクショニスト・モデル(PDPモデル)は,伝来の〈人間=機械〉を逆に反-反表象主義的機械としてネガティヴに位置づける形で,反表象主義をポジティヴに打ち出すものになるのである。そしてコネクショニスト・モデルにはさらに重要な意義がある。即ち,わたしの見るところ,〈人間=機械〉のコネクショニスト・モデルは却って〈人間知能≠AI〉("人間知能は人知を超える")を明示してしまうのである──実際,〈人間=生命〉の歴史(=コミットメントの痕跡の歴史)に対する不可知論の形で(註)。 (註) コネクショニストのAI作成はマシンに対する学習指導であり,その学習指導は,自らの理論に従うならば,人類の〈コミットメントの歴史〉をマシンに繰り返させることでなければならない。しかしこれは,〈コミットメントの歴史〉が不可知であること,および学習指導の時間の問題から,原理的に不可能である。 5.4.5 非-意味中心主義 わたしが拠って立とうとする図式(§5.4.2)は,意味中心主義に"挨拶"するときには反-意味中心主義の図式になるが,それ自体は自立した図式である。わたしは以後もしばしば意味中心主義に"挨拶"しなければならなくなるであろうが,それは,意味中心主義的な考え方との対照によってわたしの行論が際立ち,理解しやすくなると思うからである。 5.5 コミュニケーション 5.5.1 コミュニケーション 言葉でひとに働きかけることは,ひとに石を当てて働きかけることと,本質的に同じである。言葉は,"石は物理的実体である"という意味で,物理的実体である。それはひとに物理的に作用する──但し,ひとがこれに反応するということで"作用"が実現する。 石が自分に当たったとしよう。このときのわたしの反応は,状況に依って違ってくる。例えば,周りに"石を投げそうな者"が見出せたときと見出せなかったときでは,わたしの反応は異なる。わたしのこの"傾向性"は,成長の過程で形成されたものである。 コミュニケーションとは,要するに,所期の反応を相手から引き出すために,相手の傾向性を見越して石を相手に当てることである。 われわれはもちろん,石をぶつけ合うのではなく,主に言葉をぶつけ合う。しかし,石をぶつけ合ってもよかったのだ。 われわれは言葉に反応する。それは,われわれの身体が言葉に反応するように出来上がっているからだ。コミュニケーションの手段としての石に何の神秘もないように,言葉自体には何の神秘もない。神秘はわれわれの身体の方にある。 5.5.2 "言葉でコミュニケートする" 言葉でコミュニケートしているつもりは,言葉でコミュニケートしていることではない。実際,言葉は,そのとき相手に作用している諸々の物理的実体の一部であるに過ぎない。(わたしは敢えて"一部"であることを強調しよう。) 例えば,物理的実体としての言葉が音の場合,言葉のみの作用とは,聴覚器官以外の感覚器をすべて取り外した人に対する言葉の作用としてイメージされるようなものであろう。言葉がその人にとっての全存在になる。(このとき"自分"の手掛かりはどのようになるだろう?)無の中に浮かんでいる自分さえも無い状態──これが"言葉で教えている"を文字通りに受け取ったときの,それのイメージである。 言葉でコミュニケートしているつもりは,あくまでもテクスト(§2.1.2,(註2))でコミュニケートしているのである。 5.5.3 コミュニケーションの表象主義的モデル コミュニケーションに対する伝来の理解の仕方の中で,表象主義的な理解は,古典的であると同時に今日なお顕著である。 表象主義的なコミュニケーション論では,色々ある中の一つの特殊なタイプのコミュニケーションが,モデルにされている。そのモデルは,言わば"電話モデル"であり,《Aは自分の思いを言葉に託し,その言葉を相手のBに送る;Bはこの言葉からAの思いを自分の内に再現する》というものである。 "電話モデル"の偏りは明らかであるが,いま,このモデルの復習を兼ねて,偏りを例によって示すとしよう。例は,つぎのものである:
Aは(これまで見えていたことになるが見てはいなかった)一つの事象Mに,ふいに気づく。 AはMの方向を指差し,"おい,あれ!"と言う。 Bはこの結果Mを認める。 AがMに気づくことは,《Mがそこにある》を意味するような表象がAの中に作られることに対応する。さらにAの中に,《BにMを伝えるべし》という志向が対応するような表象の出来事が生起し,ついで,《Mの方向を指差し,"おい,あれ!"と言うべし》という志向が対応するような表象の出来事が生起する。そして,この志向を《Mの方向を指差し,"おい,あれ!"と言う》行為に発現させる表象の出来事が生起する。(これらの"生起"について"いかにして"は問うまい。) 表象主義のコミュニケーション・モデルは, 
われわれの例では,Bの入力として,Aの行為のほかにBの見ている風景も必要になる。そうでなければ,BによるMの認知は説明できない。実際,指差しと"おい,あれ!"の組そのものには,Mの契機は何一つないのだから。 したがって,コミュニケーション・モデルは,電話モデルに対し最低つぎのような修正を施すものでなければならない:  さて,このコミュニケーションのゴールは,Bにおける《Mの表象の生起》──《Mの認識》がこれに対応するものとして──である。しかし,この表象の生起はどのようにして可能か。上の図式において,Bに現前するテクストの表象化を"デコーディング"とはしなかったが,実際,このテクストをコードとするようなコーディングは,ここには存在していない。 さらに,テクスト(指差し,"おい,あれ!",眼前の風景,その他)からMの表象を導出する式は立たない,ということにも注意しよう。実際,このテクストからは,可能性として無限に多くのものを引き出せる筈である(空の色,雲,鳥,等々)。 われわれは以上の行論に対し,結果としての"説明不能 "よりもむしろ,つぎの事実に着目しよう。即ち,表象主義的モデルによる説明が,それの展開につれて自己解体をはじめるということ。 5.6 〈内〉 5.6.1 〈内〉の問題領分 〈内〉は二種類の問題に登場する。一つは,質量=傾向性の決定に関接する〈内〉の問題,即ち,《質量=傾向性を〈内〉によって説明する》という問題である。そしてもう一つは,場の変容の記述に関接する〈内〉の問題,即ち,《運動に随伴する場の変容のうち己れの変容に属する部分(〈内〉)を記述する》という問題であり,"運動として何が起こっているか"の問いに部分的に答える問題である。われわれは,この二種類の問題を明確に区別しよう。 第一の問題の場合,われわれの関心は先ず,場における質点の運動にある。即ち,質点がいまこれから場の中でどのような動きをするかということ,これが第一次的な問題である。そして二次的に,質量=傾向性を〈内〉によって説明するという問題が立つ。 質量=傾向性の決定に関する〈内〉の問題に対しては,わたしはつぎの二つの理由からこれを閑却する。一つは,《人間知能≠AI》(§5.4.4,(註))により,原理的に解答不能であるということ(この意味で擬似問題だということ)。そしてもう一つは,質量は質点の振舞いから伺い知れるということ。 第二の問題に登場する〈内〉は,運動の内的部面として考えられる〈内〉である。即ち,運動は大局的には場の変容であり,そして運動主体はこの場の部分をなしている。したがって,運動は,"場の部分たる運動主体の〈内〉に制限された場の変容"としての"運動主体の変容"を含意している。〈内〉の変容として捉えられるこの"運動主体の変容"はまた,焦点化する質点の変更でもある。(わたしは§2.2.2 で,この主題を"化学的"と形容した。) さて,わたしはこの第二の問題も閑却する。理由は,《善いか悪いかはともかく,われわれはこれまで"現われているもの"(overt)の把捉のみでやってきた》ということ。──但し,《"隠れているもの"(covert)が明らかにされたところで,われわれはその情報を使えない》という含意を強調点として。 5.6.2 円のメタファから点のメタファへ わたしは,認識論的主体の伝来のメタファは円であったと言おう。そしてこれを点のメタファに換えることを提案する。 こころは,伝来の認識論は円の〈内〉を埋めようとしてきた,ということである。〈内〉を埋めることが,伝来の認識論に強迫としてあった。実際,この強迫の下に,"表象"とか"スキーマ"とかCPUだとかコントローラーといった"詰め物"が開発されてきたのである。 この強迫は,円のメタファを点のメタファに換えることで無くなる。点──即ち,内がないゆえにその中に何かを書こうという気が最初から起きないところのもの。 しかしこの変更は,われわれを楽にするためのものではない。旧い強迫は新しい強迫に換わる。即ち,主体を場において語らねばならないという強迫。 5.7 教育の投機性 5.7.1 価値不可視の上の投機 新人教師は,準備不足を余儀なくされることから,どうしても機能欠損の教育(§3.6)を行なうことになる。しかし,別の意味で,機能欠損を余儀なくされているのは新人教師ばかりではない。 既に述べたように,教育の実践が従うべき教育の価値・ゴール観というものは,公けに打ち立てられていないし,また打ち立てられるものでもない。それは実践と併行して作られている──書き加え,書き直しが延々と続く性格のものである。 機能欠損の教育は,必然的に投機である。"投機"──先が見えないままに"ままよ"とやらざるを得ない,という意味において。 5.7.2 テクスト選択の投機 "教える"とは,学習者の〈低迷〉(§3.7)を適切に導いて彼の〈覚醒〉を実現することである。教師は学習者の自己燃焼を煽り,方向づける。学習者は燃焼の意識的継続によって自らの状態を高め,そして遂に"覚醒"として臨界点を突破する。 教師は"煽りと方向づけ"の目的で一つのテクストを選ぶ。この場合,教師は,伝来の知識によってあるいは自らの経験によって,そのテクストがうまくいくことを知っていてそれを選んだか,あるいは,全くの勘からそのテクストを選んだか,である。しかしいずれにしても,テクストの選択は根源的には〈投機〉である。実際,"それがうまくいくことを知っている"とは,"その投機がうまくいったことを知っている"ということなのだから。 こうして教師は,自分が選んだテクストに対して学習者が所期の反応を示してくれることに──最終的には,ある言語ゲームの主体として覚醒してくれることに──〈賭ける〉。 5.8 教材研究 "教材研究"を,わたしはつぎの二つを合わせたものとして考えることにする:
ある数学的内容を"教える"とは,学習者をある言語ゲームの主体に育てることである。(1) は,この言語ゲームを同定することである。言語ゲームは,一つの生活態xに対するxとメタ-x("x"についての論考)の二種類で考えられる。 (2) の"テクスト"には,教師の所作,教具,雰囲気といった,学習者が反応するすべてのものが含まれる。しかし勿論,完全な形でテクストを同定すること(そんなことはあり得ない)が (2) の内容ではない。われわれの"良識"が"同定すべし"と命ずるものを同定することが,その内容である。そこで実際には,教師の所作・発話と教具の同定が主になる。 これまで強調してきたように,テクストの意義は"育てるための食物"である。このとき,教師が犯しやすい間違いのパターンは,つぎの三つである:
5.9 指導案 ここで主題にする"指導案"は,"指導に先立ってそれの案をつくる"と言うときの"案"のことではない。実践的研究の成果として提出される"お勧めの指導の案"である。それは,多くの失敗を経ることで初めて得られるといったものである。 数学教育学の最終的成果は,"教える"仕方を教師に明示的に与えるものとしての,この"指導案"である。しかし,"明示的に与える"とは言っても,あくまでも,言葉(記号)の可能性の限りにおいて,ということである。このコミュニケーションは,読者である教師の傾向性を利用している。実際,指導案をわれわれは"事態の記述"のように意識して書くが,それはあくまでも,相手の傾向性を見込んでいる限りで"事態の記述"であるに過ぎない。 "事態の記述"とは何かと改めて考えてみよう。即物的にはそれは一つの形象であり,"事態"がそこに認められるわけではない形象である。しかしそれは,これを見た人が所期の形で反応することが十分予想される形象なのである。われわれはこの形象を習得した。そして,この形象の実効性が,われわれにこの形象を"事態の記述"のように思わせてしまうのである。 指導案の実効──言葉(記号)の実効として──は,相手の傾向性を見込む。これは言い換えると,《指導案はそれが読める者にしか"指導案"として実効しない》ということである。指導案を利用できる者は,何がしかの訓練(経験)を積んでいる者である。 しかし,そうだからなおさら,指導案は読者に対する作成者のコミュニケーションとして作成される必要がある。 作成者である己れを読者に理解させるというスタンスで書かれる指導案の書式は,したがって,コミュニケーションに最適な書式として決まることになる。それは例えばつぎのようになる。即ち,先ず〈単元〉について,
(1.1) 主題の数学的位置付け (1.2) ゴールとなる言語ゲーム (2) 学習者の傾向性 (3) 単元カリキュラム (4) カリキュラムの根拠 そして〈各時の授業〉について,
(1.1) 主題の数学的位置付け (1.2) ゴールとなる言語ゲーム (2) 学習者の傾向性 (3) 授業案(狭義指導案) (4) 授業案の根拠 (4) の"根拠"には,特に,多くの失敗の経験から得た教訓が根拠の形に直されて記されるであろう。
|