数の問題に還元するには,何段かの論理的ステップを踏む。 この論理的還元の概念が無かったり希薄であるとき,ひとは,量の問題から数の問題への移行をワン・ステップでやろうとする。 問題のパターンを求め,このパターンの問題に対して使うべしと習った公式を適用する。 量の問題から数の問題への移行をワン・ステップでやるやり方は,<もの→ことば>の写像論のように<量→数>の写像論を立てる論によって,合理化される。 「数は量の抽象」は,このような論である。 公式適用の問題解答は,「数は量の抽象」の立場と相性がよい。 量の問題を数の問題に還元する数学は,「数は量の比」である。 しかし,学校数学は「数は量の抽象」の方を択っている。 長方形の求積の問題解答を生徒に教えるのに,教師は「タテ×ヨコ=面積」であると教える。 速さ・時間・距離の問題解答を生徒に教えるのに,教師は「速さ=距離÷時間 (距離=速さ×時間,時間=距離÷速さ)」であると教える。 わたしの周りの学生などは,時間・距離・速さの問題を解くときはつぎの「公式」を使うようにと習ってきている; 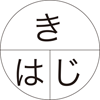
これを貫徹しようとすれば,その都度現れる論理的矛盾に対してこれを糊塗する理屈をつくりださねばならない。 こうして,「数は量の抽象」は保持しようとすればするほど,モンスター理論化する。 数学教育は,「数学から見た学校数学」の視点を重要なものとする。 学校数学は数学と同じものではないが,数学から学校数学を見ることで,学校数学が使っている「嘘も方便」が捉えられ,そして 「嘘も方便」の通用期間や,「嘘も方便」を使った報いがどのように返ってくるかということが,捉えられる。 学校数学の「数は量の抽象」を見る数学は,「数は量の比」である。 しかし,「数は量の比」は,いつも,世代的に忘却される体(てい)にある。 学校数学の歴史には,「数は量の比」対「数は量の抽象」の選択肢の立った時があった。 学校数学は「数は量の抽象」を択り,それからほぼ半世紀経つ。 「数は量の抽象」を忘却させないためには,折に触れ,これの想起に努めねばならない。 本論考はこれの一端を担おうとするものである。 |