|
"合同" の教材研究 ──導入部:存在の問題の主題化── | ||||||||||||||||
|
宮下英明(金沢大学教育学部)
長島莞一(金沢市立額小学校) 卜部義夫(金沢市立材木町小学校) | ||||||||||||||||
1.1 恣意的判断としての "ピッタリ重なる" "ピッタリ重なる" は,モノの事実ではあり得ない。二つのモノがピッタリ重なったりそうでなかったりするのではない。 "ピッタリ重なる" ということにわれわれがしたりしなかったりするのである。 "ピッタリ重なる/重ならない" は,モノの事実ではなく,われわれの都合的判断である。 但し, "ピッタリ重なる" はそうであるかそうでないかであり,中間はない。それは二値論理下の概念である。不定なのは概念ではなく,われわれの判断──二値のうちの何れを採るかの決断──である。 1.2 記号の事実としての "ピッタリ重なる" "ピッタリ重なる" はモノの事実ではない。したがって,われわれが "ピッタリ重なる" としたところのものは,モノではない。この "ピッタリ重なる" とされた存在の身分は,記号である。 1.3 "ピッタリ重なる" に対する理由づけ 記号の事実としての "ぴったり重なる" については, "理由づけ" のゲームが成立し得る。 理由づけにおいては, "ぴったり重なる/重ならない" が論理的事実に変えられるというところが,本質的である。 "ぴったり重なる" を真か偽かのものにするのは論理であるが,この論理を現わすことが "理由づけ" の本質である。 1.4 対象の述定 "ピッタリ重なる/重ならない" の理由づけは,対象の述定を比較する形でなされる。即ち, "一方はしかじかで,もう一方はしかじかである;二つのしかじかが相等(同値)[非相等(非同値)]であるので,両者はピッタリ重なる[重ならない]" ,というように。 述定無しの対象に対しては, "ピッタリ重なる/重ならない" を理由づけることはできない。 "ピッタリ重なる/重ならない" が論理的事実になるのは,述定されている対象に対してである。 実際,対象の述定無しの "ピッタリ重なる(合同)" は,公理的記述の中でしか現わすことができない。そこでは, "合同" の意味が述べられるのではなく(即ち, "合同とはしかじか" と述べられるのではなく),専ら "合同" のことばの論理が述べられる( "陰伏的定義" )。 1.5 対象の "決定条件" "ピッタリ重なる/重ならない" が対象の述定の上で理由づけられるためには,対象の述定が対象を決定するものになっていることが前提である。 そこで, "ぴったり重なる" (合同)の主題に対しては "対象の決定条件" の主題が先行しなければならないかのように,一見思われてくる。しかし,それは事実ではない。 実際, "決定する" の意味は,その条件を満たす任意の二つは "ピッタリ重なる" ということである。したがって, "決定条件" には "ピッタリ重なる" の概念が先行する。そしてこの "ピッタリ重なる" の主題は,対象の述定をつき合わせることによる対象の "ピッタリ重なる" の判定である。 このように, "ピッタリ重なる" の主題は,論理の上では,循環論になっている。この循環は,論理によって解決されるのではなく,実践の上では問題にならないという形で解決される。 1.6 対象の述定の恣意性 モノに対する "ピッタリ重なる/重ならない" の判断は,恣意である。一方, "ピッタリ重なる/重ならない" は,論理的事実としては必然である。 〈恣意〉はどこで起こっているのか。それは,対象の述定のところで起こっている。 対象の述定に対する "ピッタリ重なる/重ならない" は論理的必然であり,ここには〈恣意〉は入り込まない。〈恣意〉は対象の述定( "それはしかじかである" )のところにある。述定はフィクションであるが,このフィクションに対して推論が起こるのである。 一般に,対象を "しかじか" とするときのその "しかじか" は,恣意でしかない。真の "しかじか" はない。特に, "しかじか" については,争えない。この主題は, "図形" 指導に絶えずまとわりついている。 1.7 対象の述定としての測定 測定は,対象の述定である。対象の要素,部分,あるいは対象そのものに測定値を与えることで,対象を固定する。これが測定の意義である。 1.8 対象述定の恣意性としての測定値の恣意性 測定は対象の述定である。そして,対象述定の恣意性に,これの特殊として測定値の恣意性が応じている。 測定値は恣意である。測定値は,決まっている(実在している)のではなく,決められる。したがって恣意である。 但し, 測定値は《それは結局は決められる》という意味で恣意であるが,その一方に,誰が測っても値が或る範囲内に収まるという事実──物理的/身体的事実──がある。 この事実は, "測定値" というものが考えられることになる前提である。即ち,これが無ければ, "測定値" はもとより発想されることがない。 そこで,測定値は "こうなったもの" であると同時に, "こう決めたもの" である。 しかし, "正確に測る" が強調され過ぎるきらいのある現行の "量測" 指導では,測定値は "こうなったもの" になり易い。 "正確に測る" が強調されるとき, "正しい測定値と誤った測定値" の意識がつくられる。 "既に存るもの" としての "正しい測定値" の意識がつくられてしまう。(特に,自分の測定値と相手の測定値とで争うというナンセンスをやるようになる。) "測定値は決められる" の方が,むしろ強調されるのでなければならない。──これは, "概測" とか "測定値をまるめる" の主題ではない。実際後者では, "正確な値" が依然としてひきずられている。 測定値に対して専ら "こうなったもの" として受け止めるのではなく, "こう決めたもの" として受け止めることができるようにすることが, "量測" の重要な課題になる。 1.9 図に関する "ピッタリ重なる" 日常語の "ピッタリ重なる" は,図に対して使える。即ち, "二つの図はピッタリ重なる" の言い回しが意義をもつ。このときの "ピッタリ重なる" は, "図に関してはピッタリ重なるはあり得ない" と言うときの "ピッタリ重なる" ──論理的概念としての "ピッタリ重なる" ──とは,異なる。 2 指導内容および指導過程 2.1 指導内容 2.1.1 図に関する "ピッタリ重なる" を意識に主題化させる。 2.1.2 《二つの図の "ピッタリ重なる/重ならない" を両者のそれぞれの測定値(述定)をつき合わすことで判定する》という生活実践を,対象化させる。──但し,このときの図の述定の形態は,素材に従い, "しかじかの三角形" である。 2.1.3 "ピッタリ重なる" はモノのレベルでは成立しない概念であるということを,認識させる。 2.1.4 測定値の記述が三角形の記述であるということに,気づかせる。 図の測定は,この場合,図を "三角形" に変える意義のものになっているということを,了解させる。 2.1.5 さらにつぎのことの了解に導く。即ち, "ピッタリ重なる/重ならない" は測定値(記述)としての三角形について結論されるということ。 2.1.6 論理的必然としての "(三角形についての)ピッタリ重なる" の言い換えとして, "合同" のことばを導入する。 2.2 指導過程──4時間
3 授業 3.1 第1時 図に関する "ピッタリ重なる" を主題化させる。 3.2 第2時 3.2.1 主題 《二つの図の "ピッタリ重なる/重ならない" を両者のそれぞれの述定をつき合わすことで判定する》という生活実践を,対象化させる。 ここでは,図の述定として図の測定を実践させる。測定値が,つき合わされる述定の内容である。 図の "ピッタリ重なる" はモノのレベルでは成立しない概念であるということを,認識させる。──前時では図に関する "ピッタリ重なる" を主題化したが,本時ではこれを無効として退ける。 3.2.2 授業実践 (1) "ボール紙のアとイ 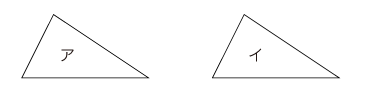
(2) "辺の長さを調べて較べるとわかる" の意見を採り上げ,辺の長さを調べる作業に入らせる。 (3) 測定して同じ長さだとした人は "ピッタリ重なる" と言い,違う長さだとした人は "ピッタリとは重ならない" と言う。人によって測定の結果(判断)が違う。 (4) ピッタリ重なる場合とそうでない場合を採り上げ,表にして書かせる。
ここで, 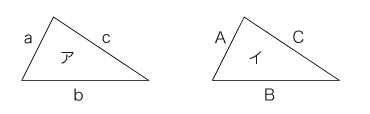
(6) "(モノとしての)ボール紙の切り抜きに対しては,ピッタリ重なるはあり得ない。" 3.2.3 授業設計での考慮事項 (1) 素材である三角形のボール紙に対し,教師は "ボール紙" の呼び方を一貫して用いる。( "三角形" とは呼ばない。) (2) "ピッタリ重なる/重ならない" を考える素材をボール紙の三角形にした理由: (2.1) モノとして,また(不完全でしかあり得ない)人為として,認識され易いようにする。厚さや紙質が意識されない紙の三角形では,《測定値は決められる》を了解させることがやり難くなる。 (2.2) 三角形にしたのは,述定が簡単であるようにするためである。ただし,このときにも矛盾する記述が起こる可能性の問題が残る。即ち, "辺の長さは両者同じだが,角の大きさは違っている" という判断が起こり得る。(この判断をなくすことが, "三角形の決定条件" の主題の一つである。)本時では, "角の大きさを調べる" の意見は認めるだけにしてとり上げず, "辺の長さを調べる" の課題へとそらしていく。 なお,矛盾する記述をはじめから起こらなくするために,三角形ではなく円にすることも考えられる。しかしこのときには,中心の問題が生じる──実際,中心を提示すれば,論理的対象としての "円" を提示したことになる( "円いモノ" ではなくなる)。 (3) 《三角形の述定のつき合わせによる三角形の合同の判定》がここでの主題であるが,もともと, "対象の合同" の教材は《対象の述定のつき合わせによる合同の判定》という形態に限られる。即ち,対象の述定無しの "対象の合同" は,教材にはなり得ない(§1.4)。 3.3 第3,4時 3.3.1 主題 前時での図の記述が三角形の記述であるということ。 図の測定は,この場合,図を "三角形" に変える意義のものになっているということ。 "ピッタリ重なる/重ならない" は測定値(記述)としての三角形について結論されるということ。 論理的必然としての "(三角形についての)ピッタリ重なる" の言い換えとしての, "合同" のことば。 3.3.2 授業実践 (1) 《(モノとしての)ボール紙の切り抜きに対して "ピッタリ重なる" はあり得ない》が前時の結論であったが,その前に "ピッタリ重なる/重ならない" の判断を出したことは事実だ。 "ピッタリ重なる/重ならない" をそのときには何に基づいて結論したのか? (自分の)測定値で判断した。 (2) 一つの測定値を固定して,全員の共通の対象にする。[前時で既に,表になったものを再現する]
(a)の場合はピッタリ重なり,(b)の場合はピッタリとは重ならないことになる。 (3) 別の場合,例えば,
のときはどうだろう。 場合(イ)ではピッタリ重なることになり,(ロ)ではピッタリとは重ならないことになる。 何と何が? 何を較べている? "3cm,4cm,5cm" の一まとまりは何? 二つの三角形だ。 三角形として,較べている。 (4) 三角形の測定値は決めた値;したがって,正しいか正しくないかの問題は起こらない。三角形については, "ピッタリ重なる/重ならない" が言える。 ボール紙について "ピッタリ重なる" はあり得ないが,三角形については "ピッタリ重なる" はあり得る。 (5) もう一度,(a)と(b)の場合に戻って考えてみよう。 このときも,較べられているのは三角形。(それが証拠に,三角形が描かれている!) 測定値を較べるときは,既にボール紙の話ではなくなっている。三角形の話だ。 (6) 測定値も,決めた値。 測定値が同じと決めたときには "ピッタリ重なる" ことになり,違うと決めたときには "ピッタリとは重ならない" ことになる。 (7) 三角形の "ピッタリ重なる" には, "合同" という言い方がある。 (8) 図の測定で,図は三角形に変えられる。 これまでしてきたことをまとめると, 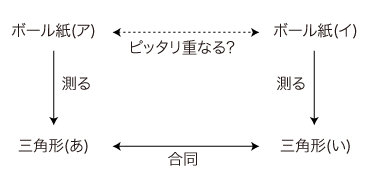
3.3.3 授業設計での考慮事項 (1) 各段階において,到達した結論を明示的に板書する。子ども間の議論をコントロールする意味でも,また主題を子どものものにしかつ彼らのうちにその内容を定着させるという意味でも,これは必須である。 (2) 図の測定は,図を三角形として記述する結果になっている。そしてこのとき, "ピッタリ重なるか否か" は,述定された三角形に関する問題── "三角形の合同" の問題──に変わっている。 (3) 実践での局面(3) は,《図の記述は三角形の記述であり, "ピッタリ重なる" かどうかの判定はこの三角形に対してのものである》の認識を起こすためのものである。 (4) 本時の主題では,三角形の決定条件が図の述定の内容になる。即ち,決定条件として十分であり,かつ矛盾しないものを図の述定として子どもから引き出さなければならない。しかし, "決定条件" の主題をこれに先行させるわけにはいかない(§1.5)。 "決定条件" をオモテに出さずに済ますためには,三角形の作図を先に指導しておき, "決定条件" を意識に上らせるということをそこでやっておくことが考えられる。また事実そうすべきである。これをしておかないと,本時の指導内容では "決定条件" が必ず何がしかの形でつまずきの問題になってくる。 (5) 本時の指導は, "測定値は決められる" という認識が既に子どものうちにあれば,やり易くなる。逆に,そうでなければ,難しい。このように,ここでの指導は "量測" 指導と関連している(§1.8)。 (6) (図の述定としての)測定の "恣意" の主題を意識に明示的に対象化させるためには, "恣意" のことば,ないしそれに代わることばが要る。ここでは, "[誰それ]が決めた測定値" の言い回しを用いている。 (7) 測定値──三角形としての述定──は恣意であるが,一旦決められた測定値に対しては, "ピッタリ重なる" か否かが(三角形の合同/非合同として)自ずと決まってしまう。 "ピッタリ重なる" か否かは,決められるのではない。選ばれた各恣意からは,必然的に "ピッタリ重なる" か否かが出る。 このことを意識に明示的に対象化させるために, "[誰それ]のように捉えたときピッタリ重なる/重ならない" の言い回しを用いる。 (8) この指導では, "ピッタリ重なる" を一貫して論理的概念として扱う。図に対して用いることのできる日常語の "ピッタリ重なる" (§1.9)は,登場させない。特に, 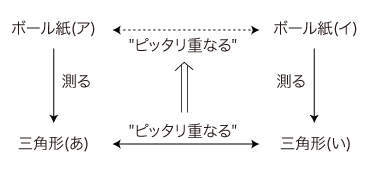
|