"図形" を,そして "図形指導" を,どのように考えるか?
発表者 金沢大学教育学部 宮 下 英 明
算数科の一領域の"図形"(以下,単に"図形")は,中学校以降の"図形" ないし"幾何"(以下,単に"幾何")と同質のものではない。"図形" は,基本的に,<モノの見方>論である。そこでは,モノとそれを見る人が出発点になる。 これに対し,"幾何" では,概念としての見方に随伴する論理が主題になる。ここでは,既にわれわれの対象になっているところの見方(概念)が,出発点になる。ここには,モノはない。 例えば,"図形" では,モノに対しての"円" という見方を指導するのに対し,"幾何" では,《"円"(=概念)には,"円周角は中心角の1/2" という含意がある》といったことを指導する。 さて,算数科の"図形" の主題になる<形=モノの見方>は,分析的な見方である。 分析的な見方とは,"しかじかのようになっている" というようにモノを見る見方である。例えば,図: 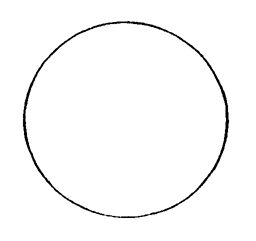
このとき形は,"しかじかであること" として,コトである。モノ(特に,図)をコトとして見るその見方である。 "図形" は,このような意味での《モノのコト化》を主題にする。他方"幾何" は,この場合のコトから出発する。それは,コトの論理系を展開する。 2. 形の恣意性 円周角が中心角の1/2であることは,"円" の定義からの推論で出てくる。円周角が中心角の1/2であることは,<論理>によって保証されている。これに対し,"このモノの形は円である" という認識を保証するものはない。 実際,図1に対し,わたしは("歪んでいる" という理由をことさらに持ち出して)これは"円でない" と言い得る。また逆に,円として 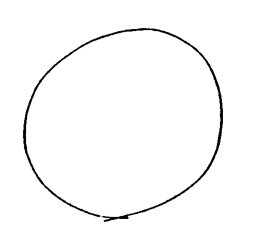
形はひとの見たものであり,ひとの都合で見られたところのものである。 そこで特に,形はモノの<属性>などではない。"マツクイムシは害虫である" とひとが言っても,マツクイムシに"害虫" という属性があるわけではない。"害虫" の判断はひとの都合であり,マツクイムシの知ったことではない。同様に,"この図は円である" とひとが言っても,その図に円という属性があるわけではない。円と見るのはそのときのひとの勝手(恣意)である。 "幾何" は<事実>を扱うが,"図形" は<事実>を扱わない。 "幾何" における<事実>とは,論理的事実のことである。事実か否かの判定の規準を論理が与えるために,そこでは<事実>を扱える。 <モノの見方>論としての"図形" は<事実>を扱えない。モノに形を見ることは,実在としてのそれの事実を取り上げることではない。形はひとの恣意であり,保証を持たない。 ところがわれわれは,形を,実在に関する事実のように,あるいはさらに実在として,考えてしまいやすい。即ち,"形というものが在る" という具合に。 形は,<形を見る>主体が見るところのものである。しかしひとは,形を考えるときに,<見る>主体の要因を看過してしまう。そして,形を,専ら見られるモノの事実のように受け止めてしまう。 繰り返すが,形は,形を見る主体の見るところのものである。そして,しかじかの形に見ることは見る主体の恣意であり,保証を持つものではない。 3. 形の承認 形の認識が恣意であり保証を持たないとはいっても,それは他者の受け容れるものであり得る。しかしそれは,保証するものを持つことによってではなく,単に,他者の承認を獲ち得ることによって,他者に受け容れられるものになるのである。(ある場合においては,図1を"円" とすることが他者に退けられ,またある場合においては,図2を"円" とすることが受容される。) "このモノの形は円である" という認識は,保証を持たない。それは,承認されるのみである。あなたが黒板に教具のコンパスで"円" を描いたり,フリーハンドで描いた"円" の上で半径や直径やらを説明したりできるのは,子どもの承認があるからである。(実際,つぎのように想像してみよ。即ち,この時点でひとりの人が授業参観の目的で教室に入ってくる;その人は黒板に描かれているフリーハンドの"円" を見て,"ハハー,このようなのは円ではないという指導をしているのだな" と思う。) ある形を見るという恣意が承認されることを,われわれは,"その見方の有効性" とか"本質的な見方" ということばで説明したくなる。しかし,この種の説明が事実に合わないことは,"図形" の指導──教師が子どもに形を承認させる──という事態を考えてみれば明らかである。さらに,"見方の有効性" は,しばしば結果論に過ぎない。また,"本質的な見方" とは,所詮 "この場合に本質的な見方" のことである。 4. <形=見方>の指導 <形=見方>の指導としての"図形" 指導は,色々な形=見方を知らせ,それを得させることが全てである。 形=見方は,《異なるモノに同じ形を見る》と《ひとつのモノに異なる見方をする》の二つの文脈で並行して指導される。実際,形を一貫してひとの都合(恣意)として扱うとなれば,その指導はこのようでなければならない。 また,形=見方は,"そのように見えてしまう"(傾性=<カラダ>)と"そのように見ようとする"(志向=<アタマ>)の往復というプロセスで獲得され,またその往復運動の形態で所有されているのでなければならない。 実際,新しい見方が自分のものになるためには,そのようには見させない既存の見方(体質)を,意識に上らせ,相対的なものとして対象化して自分から突き放すことを先ずしておかなければならない。その上で新しい見方に自らを訓練して,それをカラダにたたき込む。カラダに入るとは,<慣れる>ということ,それが何でもなくなるということである。(知識をアタマだけの事態と考える人が結構多いのであるが,この認識は全く誤っている。)しかし,この新しい体質は,やはり自己批判の形で,一つの見方として相対化して,突き放しておくのでなければならない。《このように見えてしまっているのは,このように見ているからだ》というように。これらはすべて,形を見方=人為として,ひとの恣意として,認識できるようになるためである。 《安定した身の置き場所を示すことが指導》というように考える立場があるとすれば,いま述べたのは,これと正反対のものである。ここでは,《身の置き場所はどこにもない》という認識を植え付けようとする。その認識は,《どこにも身の置き場所がないからどこに身を置くことも自由》という認識につながる。 話はここで終に,言わば,指導における教条主義への自由主義の対置というところにまで来てしまった。しかしそれは,善し悪しの問題としてではない。単に,形=見方と捉える限りそれの指導は必然的に自由主義的になる,ということが結論されただけである。 実際,わたしは"図形" 指導に関してはここでは何も主張していない。わたしは単に,形がモノの見方であることを述べ,形をモノの見方そのものとして指導するとすればそれはどのような形態のものになる筈であるかを述べただけなのである。 5. コトバとしての形 形とは,モノの見方のことである。そしてそれは,"このモノはしかじかである" という見方として,《モノのコト化》ということになる。 形は,こうしてコトとしてコトバに表現される。このとき,形とは,"xはじかじかである" という一つの文(命題関数)である。そして,文としての形は,それ自体でモノから独立している。即ち,モノの応援を必要としない。 文としての形は,論理の中にある。そしてこの論理が数学的論理(数学的語用を規定する論理)である場合に,その形は数学の対象になっているということになる。 例えば,"xは細長い" は,日常語の論理の中には収まるが,数学の論理の中には収まらない。(数学の論理は,古典的な二値論理である。"細長い" が数学の中に入るとすれば,それは,"細長い" が,細長いものと細長くないものをきっちり区分けする概念になっているときである。)これに対し,見方: 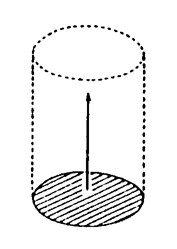
さて,われわれは,(モノにではなく)論理のみに従ってコトバを操ることができる。これはコトバを自己増殖させる営みであるが,こうして,モノから独立したコトバの世界(論理系) がつくられていく。 数学は,この<コトバの自己増殖>を自らの方法論としている。それは能う限りモノから離れて,純粋にコトバであろうとする。コトバの自律系であること,これが数学の方法論である。 数学は,日常語の改良ではない。数学と日常語は,異なる論理の上に立つ。 "円"("1点から等距離")の見方は,"まるい" の見方の改良ではない。ひとはしばしば,日常語の数学化を"正確" とか"厳密" のことばで語る。"日常語=曖昧,数学=正確" の図式を立てたがる。しかしこの認識は,誤りである。実際,数学では,"まるい" は語れない。数学は,"まるい" を受け止めることができない。 日常語の数学化は,正確化ではなく,別モノ化である。 例えば,数学の概念の"柱(ちゅう)"(図3)。これは,日常語の"柱(はしら)" の数学化であるが,この二つの見方はつぎのようにズレてしまう: ・柱(はしら)に見えなくとも柱(ちゅう): 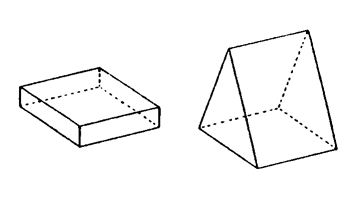
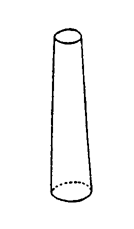
|