 PDF (280K)
PDF (280K)
「数学教育学」とは数学教育を論ずる言語行為のことであり,よって,「数学教育学」とは何か?を考えることは,「数学教育学」の言語は何か?を考えることである。 学会は,「数学教育学」の言語の制御・管理を企図する。 この企図は,一つに,特定の形の言語の囲い込みとそれ以外の言語を「ルール逸脱」にするという形になって現れる。 逸脱の言語は自ずと学会からいなくなるので,学会による「数学教育学」の制御・管理は,得失のトレード・オフをやっていることになる。そこで,このトレード・オフの妥当性が論点になる。 学会が「得」と定めるのは,グローバル・スタンダードの陣営に加わること。そしてこの方法として,「リサーチ」フォーマットをルールにする。 ルール逸脱の言語ということで「失」になるのは,実感論・経験論。「数学教育学」論も,この類になる。 研究スタイルは研究対象に応じる。 数学教育は複雑系である。 「リサーチ」フォーマットは,対象理解の形を「分析と再構成」に定める哲学──根本に,言語写像論/表象主義──に拠っている。 これは,複雑系が相手のときは,「塵を積んで山をつくるプロジェクト」になってしまう。実際,これが複雑系の複雑系たる所以である。 複雑系を相手にするときの言語は,実感論・経験論になる。 よって,「数学教育学」から実感論・経験論をなくすことはできない。
数学教育学の最初の問題は,「数学教育学」とは何か (何をすることか)?である。 実際,「数学教育学」とは何か?の問いを閑却した体(てい)で数学教育学を行うというのは,論理の上で,矛盾である。 数学教育学は,数学教育についての知見をつくる営みであり,それは言語としてアウトプットされる。 よって,「数学教育学」とは何か?の問いは,「数学教育学」とはどのような言語をつくることか?という問いになる。 数学教育の知見を述べる言語の形として実際的であるのは,実感論・経験論である。 しかしこの言語は,学会が「リサーチ」を論の形とするルールを定めるとき,所在を失う。 では,「リサーチ」が実感論・経験論の上位互換になるかというと,まったくそうでない。 それどころか,「リサーチ」の言語は,数学教育という複雑系を相手にするときの言語としては,ひどく貧困である。 そこで,「数学教育学」とは何か?を言語の問題としてこれに答えるときには,「数学教育学における実感論・経験論の位置づけ」が作業の中心になってくる。 本論考は,以上要約して述べた問題構造を論じるものである。
1.1. 研究の内容と方法 数学教育学は,(主題を大きく分けて) つぎの二つを研究する:
1.2.学会 学会は,「数学教育学」の言語の制御・管理を企図する。 具体的には,つぎのことを行う:
1.3. 研究フォーマット 学会は,学の「グローバル化」として,欧米化を志向する。 すなわち,研究の内容・方法において,欧米の先端に並び歩調を合わせることを,目指す。 「欧米化」とは,欧米方言の採用のことである。 確認:欧米も一つのローカルであり,グローバルであるわけではない。 このときの「方言」は,言語を「分析と再構築」に使うというものである。 ──欧米の学の伝統は「分析と再構築」であり,これのバックボーンとなっているのが,<リアル→言語>の言語写像論/表象主義,そしてこれに基づく合理主義・論理実証主義の哲学である。 「分析と再構築」の立場では,学はこれを方法とすることで明証性・客観性を得ることになり,研究は「明証性・客観性の実現」として取り組まれるものになる。 そしてこの理由で,「リサーチ」を研究のフォーム/フォーマットにする。 「リサーチ」フォーマットの中心は,つぎのルールである:
1.4. 言語写像論/表象主義 「学」の「欧米化」とは,欧米方言の採用のことであり,この方言の中身は言語写像論/表象主義である。 西洋哲学は非常に多様に見えても,イデア論に始まって言語写像論タイプが主流を保ってきた。 西洋哲学の中でこの主流を批判するものに,Wittgenstein の哲学 ([Wittgenstein 1958]) や Rorty のプラグマティズム ([Rorty 1982]) がある。わたしはこの考え方に与する。 Wittgenstein の説くところは:
そんなふうに使うのは倒錯である。」 ちなみに,表象主義が教育を科学すれば,人間機械論になる。 実際,「数学教育学」が範にしてきた認知科学は,人間機械論である。 ──人間知能の「分析と再構成」プロジェクトの終点は,人間知能が言語マシンの写し ( 人間知能=人工知能) になること。
2.1. ルールは<逸脱>をつくる 学の欧米化を目指すことにした学会は,学会内研究のフォームを「リサーチ」に定めることとなる。 リサーチ形式は論理実証主義に立ち,そして論理実証主義は,言語写像論/表象主義に基づいている。 表象主義は,複雑系の学とはあわない。 特に,「数学教育=複雑系」の方法論にはならない。 実際,「数学教育=複雑系」の論は,実感論・経験論の形になる他ない。 しかし,実感論・経験論は,主観論・不可知論である。 このようなものは,「数学教育学はリサーチ形式で行う」のルールに違反する。 「数学教育学からの逸脱」と位置づけられるものになる。 2.2.「数学教育学」の言語タイプ 「数学教育学」は,先ずは学会の言語現象である。 この言語現象に対しては,ロジックとして,つぎの2つの言語層/レベルが区別される:
ここで,「数学教育」論のカテゴリーに,研究フォーマット遵守と逸脱の区分を設けることにする。 このとき,研究フォーマット遵守が,学会が認めるところの「数学教育学」である。 こうして,つぎの図に示される言語タイプの別と「数学教育学」の語の3つの用法が,導かれる: 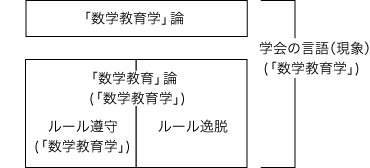
2.3.「リサーチ」形式遵守のルール化の得失 リサーチ形式のルール化で,実感論・経験論は自動的に「数学教育学からの逸脱」になる。 「数学教育学からの逸脱」は学会に棲む形ではないので,実感論・経験論は自ずと学会からいなくなる。 リサーチは,実感論・経験論の上位互換にはならない。 よって,学会は,実感論・経験論が守備領域としてきたものを失う。 ここに,リサーチ形式ルール化の得失が問題になる (「得失のトレードオフ」)。 ──「どれほどのものを得て,そしてそのかわりに,どれほどのものを失うのか?」 得るものは,主に「秩序」である。 「数学教育の発展」は,ここから得られるところのものではない。 実際,「分析と再構成」から出てくるファインディングは,「既に知っていることの押さえ」の程度にとどまる。 失うものは実感論・経験論だが,「数学学習の意義」「数学教育 (数学学習の意義を実現するものとして) の方法」の論考などは,実感論・経験論を形とするしかない (§3)。 これがごっそり無くなる。 また,「数学教育学」論も,本来思念的なものなので,「リサーチ」ルールと調子を合わせるのは難しく,やはり学会を去る。 リサーチ形式の射程は,ひどく小さい。 この小さい射程が,学会の研究射程ということになる。
3.1.「リサーチ」形式の限界の構造 研究スタイルのルールをつくるにあたっては,ある研究スタイルが想定されている。 主題によっては,そして主題に対するスタンスの取り方によっては,このルールが無意味になる。 そしてこのとき,その研究は自ずとルールを逸脱するものになる。 これが,「リサーチ」を研究フォームと定めるルールと「数学教育=複雑系」の論考の関係構造である。 リサーチで数学教育の知見を求める形式は:
こうなってしまうのは,つぎの構造的な理由による:
3.2.「数学教育=複雑系」の論考の言語 リサーチの方法は「分析と再構築」である。 そして,複雑系を相手にしたときの「分析と再構築」は,「塵を積んで山をつくる」プロジェクトになる。 それは有効な歩を進めることができないし,方向制御の方策も立たない。 ──実際,複雑系が「複雑系」であるのは,「分析と再構築」を超えるからである。 「数学教育=複雑系」の論考は,実感論・経験論になる。 そしてこれは,ルールの逸脱になる。 リサーチと実感論・経験論を対照するとき,そこでは何が見られているのか? 言語の用い方の違いが見られている。 リサーチは,言語を「対象の分析と再構成」に使う。 しかし,言語の道具性は,「対象の分析と再構成」にではなく,「意思を伝える/わからせる」にある。 そして,実感論・経験論は,言語のこの本来の使い方をしていることになる。──自分が経験的に知っていることを相手に伝える/わからせるために言語を使う。 3.3. 「数学学習の意義」の論考の場合 数学学習の個人的意義は,「成長」のことばで述べることになる。 この「成長」は,「数学学習が行われたときと行われなかったときの成長は,どう違ってくる?」という形で論ずるものになる。
この論考が意味あるものになるのは,ひとがふつう考えるときの「成長」(特に,時間スパンの長い「成長」) を考えている場合である。 ──それはつぎのような形で感得している「成長」である:
実際,リサーチが「成長」の意味にするものとは,時間スパンのごく短いものであり,ひとがふつう考える「成長」とは違う。 「数学学習の意義」の論が対象にする「成長」(=ひとがふつう考える「成長」) の論述は困難である──ほとんど不可能である。 しかし,「述べられない」は,「わからない」ではない。 実感・経験は,この「成長」を感得できる。 実際,数学学習の程度の違いが成長の違いになることは,経験的にわかる。──経験蓄積が,確信を強めていく。
この感得は,不可知論と合わさっている:
「数学学習の意義」の論考は,実感論・経験論になる。 リサーチ形式にのらない。 ──リサーチから結論として出てくる言説は,実感・経験でわかっていることの確認の程度にとどまる。 3.4.「数学の指導方法」の論考の場合 ひとが自力で,ある系を勉強しつつそこに生きることをするとき,系の意味・ロジックは,いちばん最後に理解されるものになる。 最初は,系の意味がわからず,「系の意味」の概念をもたず,ただバタバタする。 無駄なバタバタが少なくなるというのがこのときの成長である。 そしてこの成長は,たいてい,系の意味・ロジックの意識対象化 (概念化)・理解に至らないで終わる。 実際,意味・ロジックの対象化を進め,理論をつくってきたものは,<歴史>である。 ゆえに,教育が必要になる。 数学教育は,「数学」のカテゴリーで括っているところの各種<意味・ロジック>を教える。 そこで問われる。「数学の指導」は確かにこのようなものになっているか? 「数学の指導」は,たいてい,数学の指導ではない。 ──数学の指導を実現することは,簡単ではない。 では,「数学の指導」と称しているものは何か? 数学的主題の構成素材のさらに断片の「指導」である。 実際,教員のアタマの中の「数学」は,たいてい<意味・ロジック>がスッポリ抜けている。 「数学の指導方法」の論考は,「数学の指導」としては<意味・ロジック>の指導になっているものを考える。 この「数学の指導」は,長い時間スパンでとらえねばならないものになる。 また,論考は,<意味・ロジック>の抜けた「数学の指導」を現状と定めるところから,はじめねばらない。 この論考は,根柢的であるほど,(リサーチ形式にのらないという意味で)「数学教育学」の中に位置づくのが難しくなる。
4.1. 学会内──ルール遵守の形づくり (本末転倒) 実感論・経験論が学会に棲むためには,「数学教育学」のルール,特に,
実感論・経験論は,もともとルールから外れるものであり,したがって,もともとストリームをもたない。 実感論・経験論は,つぎの本末転倒のプロセスを進むしかない:
自分の論が人類の歴史の上に成り立っているということと,「研究ストリーム」の形に表現できるぐあいにその歴史を特定できるということは,別である。 実感論・経験論は,「研究ストリーム」を特定できない,また特定する意味がない。──特定するのは,ウソになる。 本末転倒を無用にするためには,<逸脱>を研究の在り方としてきちんと定めることをしなければならない。 併せて,<逸脱>の実績を積み重ねることが必要になる。 4.2. 学会外 実感論・経験論は,学会内では<逸脱>である。 したがって,本来,学会に棲めるものではない。 それらは,どこにどのようにして存るのか? (インターネットを含めても)問う術として有効なものはないというのが,いまの状況である。
「数学教育学」の研究の要諦は,数学教育を複雑系と定めたところで,その総体的とらえを失しないようにすることである。 このタイプの言語は,「数学教育学」のルールによって存在を難しくされる。 「数学教育学」は,それをどのように担保するか? この問題を考えるために,「数学教育学」を,「言語」のレベルにまで降って,改めてその実践スタイルを見直すことが必要である。 本論考は,この問題の提起であった。
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||