7.2 わり算の立式(2)
(1) 問題
つぎも算数科の問題である:
「毎秒3/2mでは何秒で4/5m」
この問題に対し「4/5÷3/2」が立式されるわけであるが,この立式の論理を満足に答えることのできる教師は,さらに少なくなるであろう。
(2) 問題の還元
この問題を時間と距離の間の比例関係の問題ととらえ得ること,すべてはここからはじまる。「毎秒3/2m」は一つの比例関係(関数)の表現である。
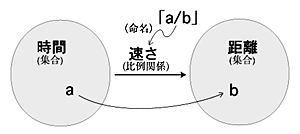
この問題を図式化すると,
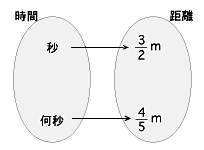
「比例関係」の含意として,
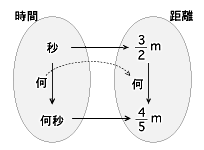
量表現「3/2m」,「4/5m」の分析として,
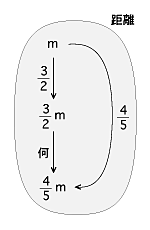
この段階で,もとの“時間と距離の間の比例関係”の問題が,“距離の倍関係”の問題
「 ((mの3/2倍)の何倍) が (mの4/5倍) か?」
に変わっている(還元されている)。
ここで「量」の含意として
((mの3/2倍)の何倍) = (mの(3/2×何)倍)
であるから,
(mの(3/2×何)倍) = (mの4/5倍)
さらにこれより,同じく「量」の含意として
3/2×何 = 4/5
こうして,最初の問題は“数の積”の問題に還元される。
(3) 式の導出
結局,求める「何」は
「3/2 とかけて 4/5 になる(分)数」
である。さらに,「3/2 とかけて 4/5 になる(分)数」の簡約した表現が「4/5÷3/2」。
以上が,最初の問題に対して「4/5÷3/2」が立式されるときの論理である。




