 ( D ⊂ ( D ⊂  ) が a ∈ D において「局所的に線形」ということ,すなわちfがaの近傍で1次関数に収束するということ,を考える。
──以下,この1次関数をfa とする。 ) が a ∈ D において「局所的に線形」ということ,すなわちfがaの近傍で1次関数に収束するということ,を考える。
──以下,この1次関数をfa とする。
「局所的に線形」は,つぎのような見方ができる: fa の傾きは, 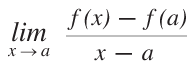
|
| Up | 局所的に線形,なめらか,接線,変化率 | 作成: 2010-10-26 更新: 2010-10-26 |
 ( D ⊂ ( D ⊂  ) が a ∈ D において「局所的に線形」ということ,すなわちfがaの近傍で1次関数に収束するということ,を考える。
──以下,この1次関数をfa とする。 ) が a ∈ D において「局所的に線形」ということ,すなわちfがaの近傍で1次関数に収束するということ,を考える。
──以下,この1次関数をfa とする。
「局所的に線形」は,つぎのような見方ができる: fa の傾きは, 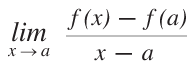
|