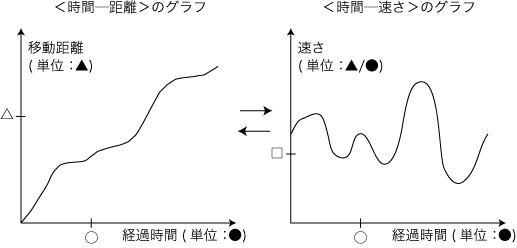
 ヒントは,「等速運動の場合」である。 等速運動であれば,小学算数の比例関係の問題になる。 実際,小学6年生はつぎのことができる: 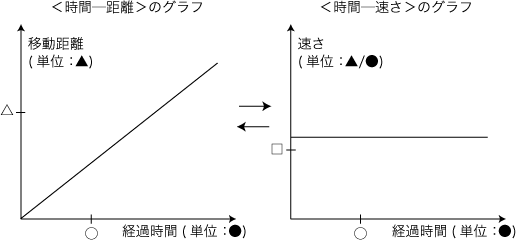 さて,これがどんなヒントになるのか? 註:「等速」の<時間─距離>グラフが直線になるのはどうして?
この3点に対しつぎの数値Δt1, Δt2, Δd1, Δd2 を考える: 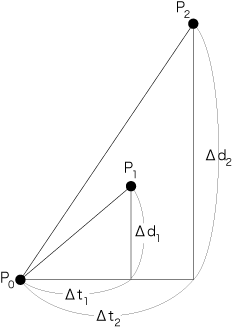
「等速」なので,Δt1:Δt2 =Δd1:Δd2。 これは,図の二つの三角形が相似(あるいは,直線P0P1 と直線P0P2 の傾きが同じ) ということ。 特に,3点P0, P1, P2 は直線上に並ぶ。 |