いま,つぎの問題を考える:
|
直線上の等速運動の「時刻と位置の対応グラフ」を作成せよ。
|
作業は,つぎの順序で進む:
- 時刻の表現
- 時刻の基準O時刻 を定め,時刻を「O時刻 から時間t」の形式で表す。
- 時間の単位u時間 を定め,時間を「u時間 の数n倍」で表す。
- 以上まとめて,時刻が「O時刻 からu時間 の数n倍」で表される。
- これの表記として,「O時刻 + (u時間 × n) 」を用いる。
- 位置の表現
- 位置の基準O位置 を定め,位置を「O位置 から距離d」の形式で表す。
- 距離の単位u距離 を定め,距離を「u距離 の数n倍」で表す。
- 以上まとめて,位置が「O位置 からu距離 の数n倍」で表される。
- これの表記として,「O位置 + (u距離 × n) 」を用いる。
- 時刻と位置の初期対応を定める
時刻「O時刻 + (u時間 × p) 」に位置「O位置 + (u距離 × q) 」が対応すると定める。
- 速さを定める
u時間 に u距離 × a が対応すると定める。
- 時刻と位置の対応の式を求める
- 時刻「O時刻 + (u時間 × x) 」に対応する位置「O位置 + (u距離 × y) 」を求める。
- O時刻 + (u時間 × p) からの経過時間は,u時間 × (x−p)
- 速さは, u時間 に u距離 × a が対応する比例関係。
よって,経過時間 u時間 × (xーp) には,移動距離 (u距離 × a) × (xーp) が対応する。
さらに,
(u距離 × a) × (xーp)
= u距離 × (a× (xーp) )
- 位置 O位置 + (u距離 × q) から 距離 u距離 × (a× (xーp) ) の位置は,
O位置 +
( (u距離 × q)
+
(u距離 × (a× (xーp) ) )
さらに,
(u距離 × q) )
+
(u距離 × (a× (xーp) )
= u距離 × (q + a× (xーp) )
- よって,y = q + a × (xーp) である。
- この式のグラフを書く
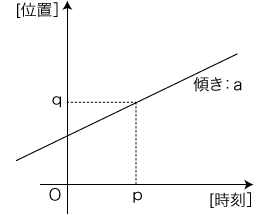
|

