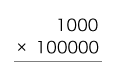
みな,つぎのように計算する: 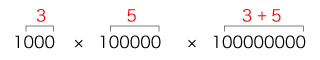
(「桁数mの数と桁数nの数の積は,桁数 m+nの数」)
学生は計算尺を買わされ,授業でこれの操作が教えられた。 この計算尺は,「かけ算を,桁数の足し算に替える」を道具にしたものである。 ここで注意だが,日常語のいう「桁数」だと,1000, 100000 はそれぞれ4桁と6桁になるが,数学だと 10‥‥0 の桁数は0の個数のことにして,1000, 100000 はそれぞれ3桁と5桁になる。 さて,「かけ算を,桁数の足し算に替える」は,どのくらいありがたいことか? 例えば,2の10乗の大きさなんかは,サッとわかってしまう。 後述するが,「桁数mの数と桁数nの数の積は,桁数 m+nの数」が成り立つように2の桁数を求めると,それはおよそ 0.3 である。 そこで,2の10乗は,桁数 0.3 の数の 10 回の積。 「桁数mの数と桁数nの数の積は,桁数 m+nの数」より,これの桁数は 0.3 × 10,すなわち 3 である。 こうして,2の10乗は,1の後に0を3個並べた数,つまり 1000 である。 実際に 2の10乗を計算すると 1024 になり,まあまあよい近似値である。 「2の10乗を実際に計算するくらいどうってことない」と思う向きは,2の100乗を考えてみたらよい。 というわけで,ここでは1から9までの桁数を求めてみる。 そして最後に,これの応用問題をやってみることにする。 なお,9までの数の桁数を求める以下の話は,わたしが大昔に読んだ森毅のテクストから拝借するものである。 (そのテクストが何だったかは,覚えていない。 『数学セミナー』? ) 以下,桁数を求めるときに用いる規則は,「mとnの積の桁数は,mの桁数とnの桁数の和」である。 1から9までの数の桁数を求める話は,これでおしまい。 ところで,ここで「数nの桁数」と言っているのは,厳密には「十進数に対する数nの桁数」である。 この言い回しは長い。 そこで,数学の短い記号表現となる。 それが,「log10n」である。 「2進数に対する数nの桁数」だと,「log2n」である。 「mとnの積の桁数は,mの桁数とnの桁数の和」は,つぎの表現になる:
高校で「log」を教えられているが,意味を教えられていないわけである。 (  「指数関数」) 「指数関数」)
もっとも,数学の授業はだいたいがこうで,「log」に限ったことではない。 応用問題 1 十進数の二進数表示は,数字の列がひどく長くなる感じがする。 どのくらい長くなるのかを,一般的に述べられないか?
これは,2のn乗である。 そして,2のn乗の桁数は,2の桁数のn倍,すなわち 0.3 × n。 十進数表示の数字列の長さは,二進数表示の数字列の長さの約 0.3 倍である。 応用問題 2 0.1 mm の紙を半分に折る。 これで厚さが2倍になる。 さらに半分に折る。──これを繰り返す。 さて,何回折ったら,月まで届く厚さになるか? ここで,月までの距離は 38万5千km。
38万5千km が 0.1 mm の何倍かを求める:
= (3.85 × 1011) mm そこで,つぎの不等式になる:
ここで,「桁数」の出番となる。 上の不等式を,桁数の不等式に替える:
3.85 × 1012 を 38.5 × 1011 に替え,38 を,桁数が計算できる 36 と 40 ではさむ:
このとき:
36 × 1011 の桁数 = (4 × 9)の桁数 + 11 = (0.6 + 0.95 ) + 11 = 12.55 = 0.3 × 41.8 40 × 1011 の桁数 = (4 × 10)の桁数 + 11 = (0.6 + 1 ) + 11 = 12.6 = 0.3 × 42 2n+1 の桁数 = 0.3 × (n+1) よって,つぎのようになる:
38.5 × 1011 の桁数 < 40 × 1011 の桁数 = 242 の桁数 したがって,「41回ではまだ月に到達しないが,42回では月を超える」が答になる。 |