| (ρ,θ)〜(ρ′,θ′) | 
| ρ=ρ′=0 あるいは ρ=ρ′かつθ≡θ′(mod 2π) |
 2,+),(
2,+),( ,+,×),×) の
,+,×),×) の 2 の要素に対する回転/倍の作用を定義しよう。
2 の要素に対する回転/倍の作用を定義しよう。
 +={x∈
+={x∈ |x≧0}として,
|x≧0}として, +×
+× の上の同値関係〜を,
の上の同値関係〜を,
| (ρ,θ)〜(ρ′,θ′) | 
| ρ=ρ′=0 あるいは ρ=ρ′かつθ≡θ′(mod 2π) |
 +×
+× )/〜をTとする。
)/〜をTとする。
 2に対する回転/倍の作用は,
2に対する回転/倍の作用は, 2の要素 (scost,ssint)(s≧0) に対するTの要素 [ρ,θ] ── (ρ,θ) の属する同値類── の作用 # として,
2の要素 (scost,ssint)(s≧0) に対するTの要素 [ρ,θ] ── (ρ,θ) の属する同値類── の作用 # として,
|
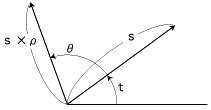
(scost,ssint)#[ρ,θ]
=((s×ρ)cos(t+θ),(s×ρ)sin(t+θ)) |
 2と同一視する:
2と同一視する:
| [ρ,θ] | ←→ | (1,0)#[ρ,θ] =(ρcosθ,ρsinθ) (ρ>0) |
 2の要素 (x,y) に対する
2の要素 (x,y) に対する 2の要素 (ξ,η) の作用としては,
2の要素 (ξ,η) の作用としては,
 2の間の二つの内算法+,×を,つぎのように定義する:
2の間の二つの内算法+,×を,つぎのように定義する:
|
(ξ,η)+(ξ′,η′)=(ξ+ξ′,η+η′)
[ρ,θ]×[ρ′,θ′]=[ρ×ρ′,θ+θ′] (ξ,η)×(ξ′,η′)=(ξ,η)#(ξ′,η′) |
|
((ξ,η)+(ξ′,η′))×(ξ″,η″)
=(ξ,η)×(ξ″,η″)+(ξ′,η′)×(ξ″,η″) |
 2の要素〉の+は,〈数ベクトルとしての
2の要素〉の+は,〈数ベクトルとしての 2の要素〉の+と同じ。〈数ベクトルとしての
2の要素〉の+と同じ。〈数ベクトルとしての 2の要素〉に対する〈作用素としての
2の要素〉に対する〈作用素としての 2の要素〉の作用#は,〈作用素としての
2の要素〉の作用#は,〈作用素としての 2の要素〉の間の×と同じ。そして,+と×は,加法と乗法の関係にある。
2の要素〉の間の×と同じ。そして,+と×は,加法と乗法の関係にある。
 2,+,×) は (0,0) を零元,(1,0) を単位元とする可換体になる。(x,y) の対称元が (−x,−y) で,[r,θ]≠0の逆元が [r-1,−θ]。
2,+,×) は (0,0) を零元,(1,0) を単位元とする可換体になる。(x,y) の対称元が (−x,−y) で,[r,θ]≠0の逆元が [r-1,−θ]。
 2,+,×) は数の系になる。
2,+,×) は数の系になる。
 2,+,×) の要素 (ξ,η) に対する (
2,+,×) の要素 (ξ,η) に対する ( ,+,×) の要素ζの作用が
,+,×) の要素ζの作用が
| (ξ,η)×ζ=(ξ×ζ,η×ζ) |
 2,+,×),(
2,+,×),( ,+,×),×) において,
,+,×),×) において,
| 1=(1,0),i=(0,1) |
| (ξ,η)=1×ξ+i×η |
 2,+,×) は実数体 (
2,+,×) は実数体 ( ,+,×) の上の二元体。そこで,数の系 (
,+,×) の上の二元体。そこで,数の系 ( 2,+,×) を(“二元数の系”の意義から)“複素数”と呼ぶ。またこの系の中の
2,+,×) を(“二元数の系”の意義から)“複素数”と呼ぶ。またこの系の中の 2を
2を と書く。
と書く。
|
(x,y)#(ξ,η)
=(scost,ssint)#[ρ,θ] =(sρcos(t+θ),sρsin(t+θ)) =(sρ(costcosθ−sintsinθ), sρ(sintcosθ+costsinθ)) =((scost)(ρcosθ)−(ssint)(ρsinθ), (ssint)(ρcosθ)+(scost)(ρsinθ)) =(x×ξ−y×η,y×ξ+x×η) |