自然数 → 整数 → 有理数 → 実数 → 複素数 → 四元数 の流れでは，実数のところから，実線型空間を量にしていきます。
また一方，自然数 → 正負の数 (整数, 有理数) → 実数 → 複素数 → 四元数の流れでは，正負の数のところから，「位 (位置)」の概念が立つようになります。(  「位」表現──存在の３態：位・量・数 )
量が実線型空間のとき，位は実線型空間に対応する実アフィン空間になります。
ここで「実線型空間に対応する実アフィン空間」の意味ですが，つぎのようになります：
|
線型空間に対しては，「点」を要素とするアフィン空間が考えられます。
１次元実ベクトル，２次元実ベクトル，３次元実ベクトルをそれぞれ「直線上の移動/シフト」,「平面上の移動/シフト」,「空間の中の移動/シフト」と見てきましたが，このとき暗黙に対象化していた直線，平面，空間の身分を表すことばが，「アフィン空間」です。
そして特に，実線型空間に対応するアフィン空間を「実アフィン空間」と呼びます。
実アフィン空間では，点の表現が主題になります。そして，
「原点と定めた点Ｏから移動ベクトルｑだけシフトしている点Ｐ」
が，表現の形になります。
式にすると，つぎのようになります：
P ＝ O ＋ ｑ
|
１次元では，点の表現がつぎのようになります：
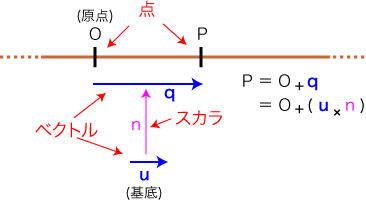
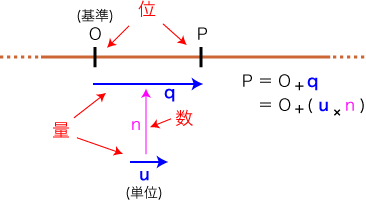
実際，１次元では，量と線型空間が同じものになったように，位とアフィン空間が同じものになります。
特に，つぎの対応が成り立っています：
| 位・量・数 |
点・ベクトル・スカラ |
| 「基準・単位」 |
「原点・基底」 |
つぎに２次元では，点の表現がつぎのようになります：
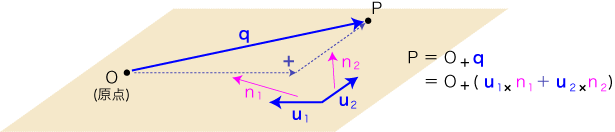
確認：
- 点 ：P, O
- ベクトル：ｑ,
ｕ1,
ｕ2,
ｕ1 ｘn1,
ｕ2 ｘn2
- スカラー：n1, n2
２次元以降では，量と線型空間が構造の違うものになりますので，位とアフィン空間も構造の違うものになります。
ただし，緩い対応関係として，１次元に引き続きつぎの対応関係を見ていくことができます：
| 位・量・数 |
点・ベクトル・スカラ/行列 |
| 「基準・単位」 |
「原点・基底」 |
なお，点の表現の枠として用いている基底と原点の組──２次元の場合だと ( (ｕ1, ｕ2), Ｏ ) ──を，「(アフィン)枠」と呼びます。
|