1次元実線型空間は,構造においても,実数に対する量と同じものになります。 すなわち,1次元実線型空間と実数に対する量は,同じものです。 しかし,2次元以上では,線型空間と量は,構造において異なるものです。 (最も特徴的な違いは,量は1次元であるということ。) すなわち,線型空間と量は違うものです。 特に,量は線型空間の低次元版ではありません。 ──逆の言い方をすれば,線型空間は量の次元拡張ではありません。 以下,1次元では同じものになった線型空間と量が,2次元以上になるとどのような違いを示すことになるのかを,見ていくことにします。 1次元実線型空間では,量であるところのベクトルは,直線上の移動/シフトになっています: 
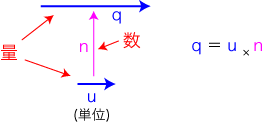
1次元が2次元になると,「直線上の移動/シフト」は「平面上の移動/シフト」になります。 そして,線型空間の要素としてのベクトルの表現が,つぎのようになります: 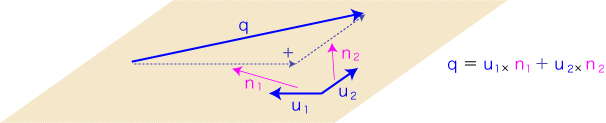
直線上の移動/シフトは,単位の何倍という形で記述できました。これに対し平面上の移動/シフトの場合,「数」ではなく「スカラー」で表現を行おうとすると,単位は成立しません。 単位の役割をさせるものとして,向きの異なる2つのベクトルの組 (u1, u2) を用いることになります。 実際,上図のように,どの移動/シフトも
なお,このように用いられるベクトルの組のことを,「基底」と呼んでいます。 3次元は,ベクトルが「空間の中の移動/シフト」になります。 これを表現するには,向きの異なる3つのベクトルの組が必要です。 すなわち,向きの異なる3つのベクトルで基底をつくることになります。
量を単位の何倍で表すことには,ベクトルを基底の行列倍で表すことが対応します。 量では数が単位に対する倍作用素であるのに対し,線型空間では行列が基底に対する倍作用素になるわけです。 こうして,2次元以上では,「スカラー」と「行列」の二本立てで「数」の機能を賄っていくふうになります。 |