 度数分布
度数分布
棒グラフは離散型分布のグラフであり,ヒストグラムは連続型分布のグラフである。 どういうこと? 関数の積分は,区分求積の極限で定義される。 区分求積は,関数を階段関数に近似する。 この階段関数が,ヒストグラムである。 実際,「ヒストグラム」の主題は,「微分・積分」である。 ──「ヒストグラム」は,「微分・積分」の初等版である。 ヒストグラムは,つぎのようになっている: 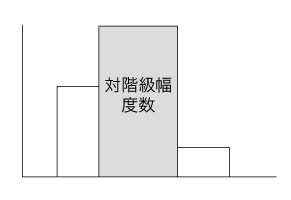
度数の変化率である。 「柱の高さは度数の変化率」が「度数は柱の面積」と対応している。 これは,速さの時間変化のグラフで,グラフの面積に距離が表されるのと,同じ理屈である。 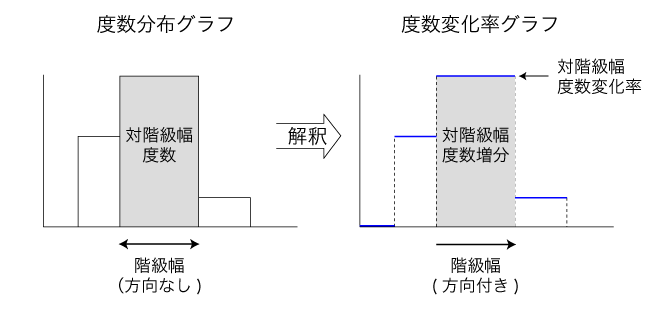
そしてこのときは,柱の面積と柱の高さが,同じ値になる。 そこで,「柱の高さが度数を表している」の誤解となる。 「度数は柱の面積に表される──柱の高さは度数の変化率を表す」をとらえ損ねることになるわけである。 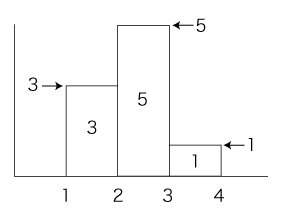
製品の米袋から米粒100個を抽出し,1粒の重さの平均を求めるとする。 1粒の重さの階級をつくって,「△グラムから□グラムの間の重さの米粒は○個」のヒストグラムをつくった: 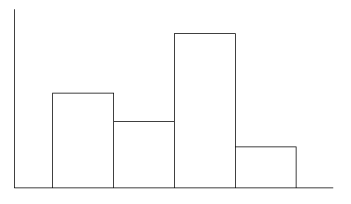
つくってみて,階級の幅が大き過ぎると感じた。 そこで,階級幅の細分を行った。 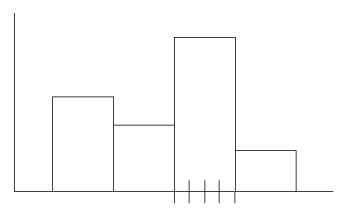
このとき,各柱の高さはどうなるか? つぎのような感じになる: 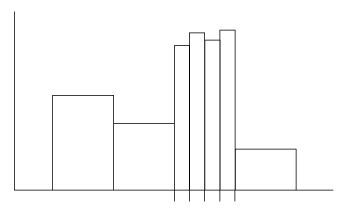
しかし,「柱の高さが度数」と勘違いしていたらどうなるか。 「階級幅をn等分したときの新しい柱は,n分の1の高さになる」になってしまう。 上のグラフのようにはならないわけである。 ヒストグラムのロジックは,なかなか理解されない。 なぜか? このロジックは,「連続型」のロジック──「微分・積分」──である。 そして,「連続型」のロジックは,実際,難しいのである。 あるいは,カラダになかなかしっくりこないロジックだということになる。 |