「数は量の抽象」は没理論である。
この没理論を見て取れるためには,「数・量」の数学の知識が必要になる。
「数・量」の数学は,「数は量の比」の数学である。
そこで,「数は量の抽象」の論を見る前に,「数は量の比」の数学の押さえておくことにする。
( 「数・量」の数学的定義 ) 「数・量」の数学的定義 )
- 数学では,数も量も形式である (形式として定義される)。
そして形式ということでは,以下に示すように,数が量より先にくる。
- 数 (一つの系) の形式は,要素の集合N,加法+,乗法× で構成される:
例: 自然数 (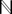 , +, ×),
有理数 ( , +, ×),
有理数 ( , +, ×),
複素数 ( , +, ×),
複素数 (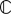 , +, ×) , +, ×)
- 量 (一つの系) は,数を作用素とする加法群のように定義される。
これの形式を示すのに,「普遍対象 (universal object)」の考え方を使う。
すなわち,(N, +, ×) の要素を使ってつくられるつぎの対象を,「数 (N, +, ×) を作用域とする量」の普遍対象にする:
読み方:
「(N, +, ×) の要素 が,(N, +) の要素に,倍作用 (真ん中の × )する」
量 (系) は,「数 (N, +, ×) を作用域とする量」として,( (N, +), ×, (N, +, ×) ) と同型な対象 (object) として定義される:
( (Q, +), × , (N, +, ×) )
読み方:
「(N, +, ×) の要素 が,(Q, +) の要素に,倍作用 ( × ) する」
| 例: | ( (りんごの個数, +), × , (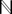 , +, ×) ) , +, ×) )
( (重さ, +), × , ( +, +, ×) ) (分数値に限定の場合) +, +, ×) ) (分数値に限定の場合)
( (直線上の移動, +), × , ( , +, ×) ) , +, ×) )
( (平面上の移動, +), × , (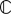 , +, ×) ) , +, ×) )
|
(Q, +) の要素が,量(要素) ──「量(系)」に対する「量(要素)」──である。
量(要素) に関する算法としては,量(要素) 同士の和と,量(要素) に対する数(要素) の倍だけが定義される。
量(系) と量(要素) の区別の意味:
個々の重さが量(要素)で,個々の重さを要素とする集合 (「重さ」のカテゴリーに対応) が量(系)。
特に,量の構造は数の構造より導かれる。
例えば,量の位相構造は数の位相構造から導かれる。
──自然数,有理数,実数を作用素とする量の位相は,それぞれ離散,稠密,完備である。
そして,以上のこととあわせて,つぎのことを確認しておく:
- 量は自体的に存在していない。
人が,物(たとえば,棒)に,量(たとえば,長さ)を解釈する。
量のその解釈がどのようになるかは,人と物 (すなわち状況) に依存する。
|
 「数・量」の数学的定義 )
「数・量」の数学的定義 )
 「数・量」の数学的定義 )
「数・量」の数学的定義 )