( (N, +), ×, (N, +, ×) ) は,Nの要素を倍の作用素として考えるすべての量 ( (Q, +), ×, (N, +, ×) ) にとって,この量の構造を示すものになっている。 数学のことばを用いれば,
「普遍対象」は,イデア論の「イデア」である。 ( (N, +), ×, (N, +, ×) ) は <Nを作用域とする量>のイデアであり,イデア ( (N, +), ×, (N, +, ×) ) の降りてきたものが <Nを作用域とする量>である。 ──実際,数学で自体的に存在するのは,数であって,量ではない。 線型空間論で「体K上のn次元線型空間E」を少し進んだところで,
「線型空間EとKnの同型」 ただし,「線型空間」と「量」は同じではない。 例えば,自然数 ( 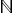 , +, ×) に対する量 ( ( , +, ×) に対する量 ( (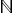 , +), ×, ( , +), ×, (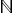 , +, ×) ) は,線型空間ではない。スカラが実数の2次元実線型空間 ( ( , +, ×) ) は,線型空間ではない。スカラが実数の2次元実線型空間 ( (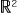 , +), ×, ( , +), ×, (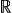 , +, ×) ) は量ではないが,複素数をスカラとしたときの1次元の線型空間 ( ( , +, ×) ) は量ではないが,複素数をスカラとしたときの1次元の線型空間 ( (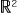 , +), ×, ( , +), ×, (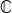 , +, ×) ) は,( ( , +, ×) ) は,( (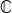 , +), ×, ( , +), ×, ( , +, ×) ) と同型なので,量である。 , +, ×) ) と同型なので,量である。
|