Up 学校数学は「数は量の抽象」を択る  

    学校数学は「数は量の抽象」を択っていることになる。

      例：正負の数
        現行では，正負の数は「正逆２方向の量の抽象」として指導される。
        数学であれば，正負の数はつぎのように「正逆２方向の量の比」として指導されねばならない：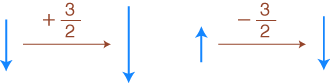


        そしてこのように指導されるとき，「負数 × 負数＝正数」はアタリマエのことになる：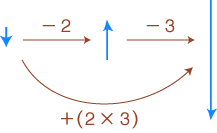


        しかし，学校数学は，正負の数を「正逆２方向の量の抽象」で指導するので，「負数 × 負数＝正数」の説明ができない──荒唐無稽なこじつけがこの場合の「説明」になる。


    「数は量の抽象」論を構成する以下のものも，すべて現行の学校数学および数学教育の学会の中に現象としてある：

      「数は抽象，量は具体」
      「量には内包量と外延量がある」
      「数の積は量の積の抽象」
      「数指導はタイルで」
      「割り算には等分除と包含除がある」
      「形式不易の原理」
      「１と見る」

    　註： タイルは，タイルという形状に意味があるわけではない。 おはじきであろうと竹ひごであろうと，「数は量の抽象」の図式に立つものであれば，タイルと同じことである。 (「数指導はタイルで」)

    つまり，結果として，学校教育に入ったのは，「割合論争」で遠山が主張した「数は量の抽象」である。 ──和田の「数は量の比」は，学校教育には容れられなかった。