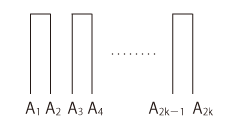
- つぎの問題を考える:
2k 本のひもがある:
上辺と下辺のそれぞれで,端を2つずつ結ぶ。
このとき,全体で1つの環が出来上がる確率Pを求めよ。
|
Pは,つぎの数N,Mに対する M/N である:
(1) このときの結び方は,N通り。
(2) このうち,全体で1つの環が出来上がる結び方は,M通り。
- Pは,つぎの問題のPと等しい:
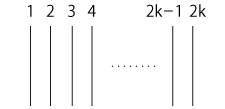
k 本のひもがある:
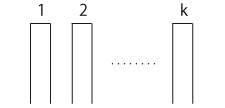
端を2つずつ結ぶ。
このとき,全体で1つの環が出来上がる確率Pを求めよ。
|
Pは,つぎの数N′,M′ に対する M′/N′ である:
(1) このときの結び方は,N′ 通り。
(2) このうち,全体で1つの環が出来上がる結び方は,M′ 通り。
- ひもの端に,つぎのように記号をふる:
N′ は,つぎの N′ と等しい:
(1) A1, A2, ‥‥, A2k−1, A2k をペアに分ける。
分け方は,N′ 通り。
また,m=3のときは,M′ は,つぎの M′ と等しい:
(2) A1, A2, ‥‥, A2k−1, A2k をペアに分ける。
{A1, A2}, ‥‥, {A2k−1, A2k} のいずれも含まない分け方は,M′ 通り。
(m=3の場合)
問題:
6本のひもがある:

上辺と下辺のそれぞれで,端を2つずつ結ぶ。
このとき,全体で1つの環が出来上がる確率Pを求めよ。
|
解答:
Pは,つぎの問題のPと等しい:
3本のひもがある:
端を2つずつ結ぶ。
このとき,全体で1つの環が出来上がる確率Pを求めよ。
|
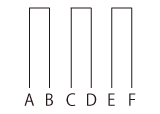
ひもの端に,つぎのように記号をふる:
Pは,つぎの問題のPと等しい:
文字 A, B, C, D, E, F をペアに分ける。
{A, B}, {C, D}, {E, F} のどれも含まない分け方になる確率Pを求めよ。
|
A, B, C, D, E, F をペアに分ける仕方は,つぎの 15 通り:
{A, B} ─ {C, D} ─ {E, F}
─ {C, E} ─ {D, F}
─ {C, F} ─ {D, E}
{A, C} ─ {B, D} ─ {E, F}
─ {B, E} ─ {D, F}
─ {B, F} ─ {D, E}
{A, D} ─ {B, C} ─ {E, F}
─ {B, E} ─ {C, F}
─ {B, F} ─ {C, D}
{A, E} ─ {B, C} ─ {D, F}
─ {B, D} ─ {C, F}
─ {B, F} ─ {C, D}
{A, F} ─ {B, C} ─ {D, E}
─ {B, D} ─ {C, E}
─ {B, E} ─ {C, D}
このうち {A, B}, {C, D}, {E, F} のいずれも含まないのは,つぎの7通り:
{A, C} ─ {B, E} ─ {D, F}
─ {B, F} ─ {D, E}
{A, D} ─ {B, E} ─ {C, F}
{A, E} ─ {B, C} ─ {D, F}
─ {B, D} ─ {C, F}
{A, F} ─ {B, C} ─ {D, E}
─ {B, D} ─ {C, E}
よって,P=7/15
註:赤色の部分は,生徒への説明が難しいところである。
|