- 「多角形の内角の和」を主題化する最初の発問は,「n角形の内角の和は?」ではありません。
「n角形の内角の和は?」と問えるのは,すでに
「形(大きさ)の違いによらず,n角形の内角の和は一定」
がわかっているときです。
数学的には,「形(大きさ)の違いによらず,n角形の内角の和は一定」のところから,問題にしなければなりません。
それに指導の上からも,「形が大きくなれば内角の和も大きくなる」と考える子どもがいることを想定すべきです。
そこで,最初の発問は,つぎのものでなければなりません:
「この二つのn角形では,内角の和はどちらが大きい?」
そして,この問題の解決の中に,つぎの内容が含まれてくることになります:
「形(大きさ)の違いによらず,n角形の内角の和は一定。
そしてそれは (180 × n − 360) 度」
- n角形の内角の和を求める方法には,巧拙があります。
また,万能の方法は,「外角」を用いる方法です。
このことを,確実に指導内容に含めなければなりません。
内角の和を求める方法の導入順序は,つぎのようになります:
「三角形に分割」の指導では,「三角形に分割」の巧拙を出します。
「拙」から「巧」への順番は,つぎのようになります:
- 対角線を任意に引いて,三角形分割
- 一つの頂点から残りの頂点に対角線を引いて,三角形分割
- 三角形の内部に一点を定め,これから頂点に線をひいて,三角形分割
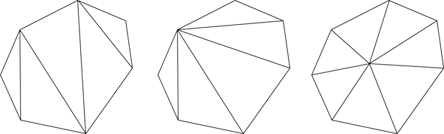
「1=拙,2=巧」の理由
1は,実験にしかなりません。
2 は,三角形の個数を論理的に出せます。
(内角の和は,180゜に三角形の個数 (nー 2) を掛けて得られる。)
「2=拙,3=巧」の理由
3は,「辺の数=三角形の数」なので,三角形の個数をとらえるのが簡単です。
(内角の和は,180゜に三角形の個数 n を掛け,中心の 360゜をマイナスして得られる。)
また,「1=拙,2=巧」を主題化するためには,nを6以上にする必要があります。
(5角形では,「一つの頂点から残りの頂点に対角線を引く」しかありません。)
- 方法2と3は,n角形が凸図形でないときに,行き詰まります。
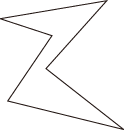
このとき,万能の方法として,外角を使う方法の登場になります。
すなわち,「三角形分割=拙,外角を使う=巧」の位置づけとなります。
外角を使う方法では,内角の和は,
180゜にnを掛け,外角の和 (=360゜) をマイナスする
で求めることになります。
この方法が最後にくるのは,外角の考え方・つくり方がけっこう難しいからです。
── 凹図形で試してみると,難しさがわかります:
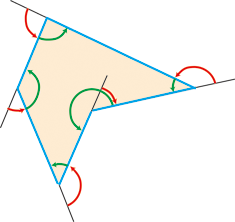
(凹んだところでは,外角が内に入ってくる)
「外角の和は,nに依存せずつねに 360゜」は,つぎのように指導するのが,学習者にとってわかりやすいでしょう:
n角形を一周してごらん。
外角は,方向転換と同じだ。
1周して最初の体勢に戻るとき,カラダはちょうど1回転している。
つまり,外角の和は 360゜だ。
|