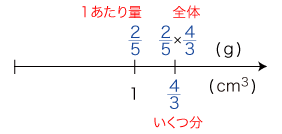
数の積の意味が生徒に伝えられる形は,一つが「かたまり × いくつ」であり,そしてもう一つが,つぎの「数直線」が説明図式として用いられるところの,「1あたり量 × いくつ分」である:
以下,この「1あたり量 × いくつ分」の数学を示す。
体積(系),重さ(系) を,( (Q体積, +), ×, (N, +, ×) ),( (Q重さ, +), × とする。
体積と重さの間の比例関係全体は,量になる:
( (Hom( Q体積, Q重さ), +), ×, (N, +, ×) )
ここで,
- f, g ∈ Hom( Q体積, Q重さ) に対し,
(f + g)( x ) = f( x ) + g( x ) ( x ∈ Q体積 )
- f ∈ Hom( Q体積, Q重さ),n∈ N に対し,
(f × n)( x ) = f( x ) × n ( x ∈ Q体積 )
|
「1あたり量 × いくつ分」は,「×」の意味を,Hom( Q体積, Q重さ) × Q体積 の Q重さ への写像:
( f, x ) ├─→ f( x ) ( f ∈ Hom( Q体積, Q重さ),x ∈ Q体積 )
|
に定めていることになる。
なぜ,ここで「×」の登場になるのか?
この写像 (Fとする) は,複比例関数になっている。
そして,Q体積 と Q重さ の単位を定め,この単位に準じて Hom( Q体積, Q重さ) の単位を定めるとき,Fから導かれる数値の関数:
( 体積単位あたり重さの数値,体積の数値 ) ├─→ 重さの数値
は,2数にその積が対応するものになる:
例えば,体積の単位に cm3,重さの単位に gをとるときは,g/cm3 を Hom( Q体積, Q重さ) の単位にする。
このとき,
F( g/cm3 × 2,
cm3 × 3 )
= ( g/cm3 × 2 )
( cm3 × 3 )
= (g/cm3) (cm3 ) × ( 2 × 3 )
= g × ( 2 × 3 )
この結果を見て,「×」を使っているわけである。
このように,「1あたり量 × いくつ分」における数の積の立式は,これを数学にすると,「F(f, x) に対する数の積の立式」ということになる。
もっとも,「数の積は量の積の抽象」の立場では,数の積の立式は直接的であり,式の導出の明証は無用のものになる。
実際,「抽象」を謂う所以である。
「抽象」は,「存在の事実の捉えとこれの記述」であるから,明証するというものではないわけである。
| 註 : |
「1あたり量 × いくつ分」は,「数の積は量の積の抽象」の立場である。
そして,「数の積は量の積の抽象」の立場は,<数は量の抽象>の立場である。
<数は量の抽象>は,「量の積」として「1あたり量 × いくつ分」の概念を立てる。
そして,この「量の積」の意味を,「内包量と外延量の積」とする。
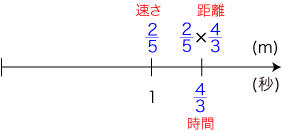
「内包量」が「1あたり量」と同じものであることを,「速度」を例に,見ておこう。
「速度」は,<数は量の抽象>の立場において,内包量となる。
そして,「速度」の図式は,つぎのように「1あたり量」の図式に他ならない:
ところで,「内包量」は,「足せない」で特徴づけられている。
特に,内包量である速度は,足せない。
一方,「内包量」は,比例関係に他ならない。
したがって,これは量になる。
足したり倍したりできる。
実際,われわれは,速度を日常的に足したり倍したりしている。
このように,「内包量」は,<数は量の抽象>が自家撞着を曝す主題になっている。
ただし,この自家撞着を見て取るには,数学が必要になる。
|
|