- 小学校・中学校で「グラフが直線になる関数」を勉強しました。
──小学校で「f(x)=ax」,そして中学で「f(x)=ax+b」。
- ここで,
「一般の関数 f(x) を扱えるようになりたい!」
という欲が出てきます。
しかし,これは欲張り過ぎ ^^;
「1次関数」のつぎということで「2次関数」に取り掛かるというのはどうでしょう。
控えめでいいアプローチです ^^
この順序で行くと,3次関数,4次関数,そして一般n次関数と進むことになります。
しかしここでは,もっと欲張って,「→2次→3次→‥‥→n次」のステップを跳び越えることにします。
すなわち,n次関数の「なめらか=局所的に1次 (線型)」という特徴に着目します。そして「n次関数」を跳び越えて,つぎのように欲張っちゃいます:
「グラフがなめらかな曲線になる関数」を扱えるようになりたい!
- 「グラフがなめらかな曲線になる関数」からは「傾きの変化のグラフ」が導かれます。
- 「傾きの変化のグラフ」の概略を簡単に求めたいなら,つぎのようにします:
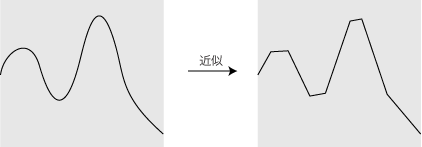
なめらかな曲線のグラフを,直線でつなぎあわせた形に近似する。
(1次関数をつないだ形に近似する。)
要するに,小学生が処理できる形に直し,自ら小学生になって処理しようということです。
──「難しいものは,簡単なものに置き換える!」
|

