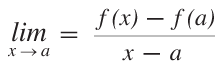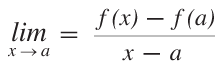- 関数 f (のグラフ) がなめらか(=局所的には「限りなく直線」)であるとき,その直線をどのような式の直線と定めたらよいでしょうか。
- 先ず,「なめらか」を示す直線は場所によって違うわけですから,「なめらか」を「点Pにおいてなめらか」という言い方で限定しましょう。
- 「点Pにおいてなめらか」を示す直線 (以下,Lとします) は,点Pを通ります。
(なぜなら,点Pを通らない直線は,点Pに目を近づけるにしたがい視野の外に出てしまいますから,Lにはなれません。)
- つぎに,関数 f のPでの変化率(xの変化に対するf(x)の変化の割合)が,Lの傾きになります。
(なぜなら,傾きが f のPでの変化率と等しくない直線は,Lと交差する直線の外観を呈しますから,Lにはなれません。)
- 点Pでのxの変化Δに対するf(x)の変化の割合は,一般にΔの取り方によって違ってきます。そこで,関数 f のP(a, f(a)) での変化率を,つぎのように (平均変化の極限として) 定義します:
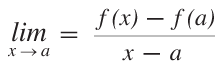
|