Up 準備 : 「移動」の運動の記述 作成: 2011-02-04
更新: 2011-02-04

    この章は，「移動」の運動の解析が主題である。 「移動」の運動のデータの記述・解析を考えようというわけである。

    「移動」の運動の記述ということでは，小学校以来「時間と距離の対応」をやってきている。
    この対応を，表やグラフに表してきた。
    さらに，この対応を「関数」としてとらえ，グラフを「関数グラフ」のように考えることもやってきている。

    ところが，この表やグラフの表現というのが，しくみ/論理が存外難しい。
    このしくみ/論理を改めて問われて，数学的にきちんと言える者は，ほとんどいないと見てよい。
    そこで，この章の本題に入る準備として，表・グラフ表現のしくみ/論理を最初に押さえておくことにする。


    「移動」の運動のデータとしての「時間と距離の対応」は，意識としては，「時点と地点」の対応である。 そして，「時点と地点の表現」「時間と距離の表現」の課題を (意識的あるいは無意識的に) 処理して，データをつくっている。
    すなわち，以下のように：

    1. 時点と地点をつぎのように表現する：
      時点を,「基準とする時点ＯT から時間ｔだけ隔たった時点」の形に表現する。
      地点を,「基準とする地点ＯＰ から距離ｄだけ隔たった地点」の形に表現する。
    2. そして，「時点と地点」の対応を，データでは「時間と距離」の対応で記述する。
    3. ここで「時間と距離」の対応の記述であるが，これはつぎのように処理している：
      時間を,「単位とする時間T の＜数＞倍」の形に表現する。
      距離を,「単位とする距離ｕＤ の＜数＞倍」の形に表現する。
    4. そして，「時間と距離」の対応を，データでは「単位ｕT に対する数値と単位ｕＤ に対する数値」の対応で記述する。

    なお，時点の基準ＯT と地点の基準ＯＰ のとり方は任意であるから，時間ｔ，距離ｄは「有向」で考えることになる。
    そしてこれより，単位ｕT に対する数値と単位ｕＤ に対する数値は，正負の数になる。──実際，ふつう実数で考えている。

    このデータをグラフにするときは，さらに，＜時点─時間─数＞と＜地点─距離─数＞を，直交するグラフの軸と同一視する作業を (意識的あるいは無意識的に) やっている。
    「同一視」は，数学的にいえば「同型 (isomorphism) を立てる」ということである。


    以上の作業によって，つぎの枠 (座標系) に到達する：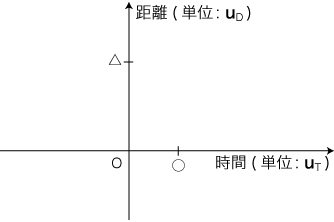



○，△は，０でない任意の数。
原点Ｏが，ＯT とＯＰ の両方に対応。

    そして以後，この枠にしたがって「移動」の運動のデータをグラフにしていく。

    さて，グラフの始点は運動の起点ではない。データ取りの開始点である。
    初学者は「グラフの始点は運動の起点」と誤解する/間違うことが多いので，ここでしかと強調しておく。

    運動のデータは，ＯT ，ＯＰ のとり方に依存して数値が違ってくる。よって，グラフ枠でのグラフ曲線の位置も違ってくる。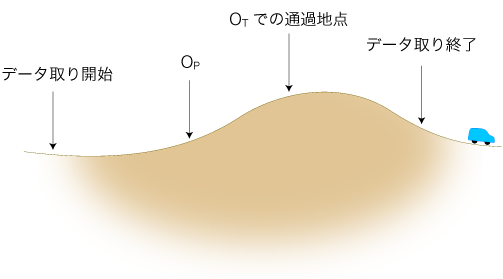




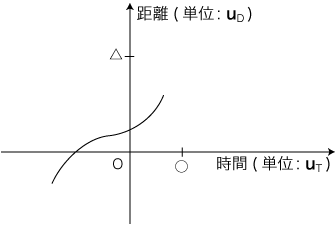
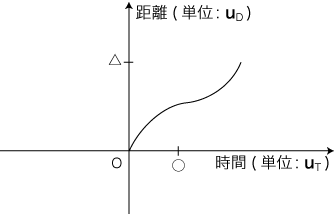
    一方，グラフ曲線の形は ＯT ，ＯＰ のとり方に依らず同じであるから，ＯT ，ＯＰ のとり方のいろいろには，互いに平行移動して重なる関係にあるグラフ曲線のいろいろが対応する。


    もっとも，通常はグラフの始点を枠の原点に設定するが，これは簡単・便利のためである。 ──この＜簡単・便利＞も，ここで述べてきた＜しくみ/論理＞の理解の上に了解されていることが必要である。