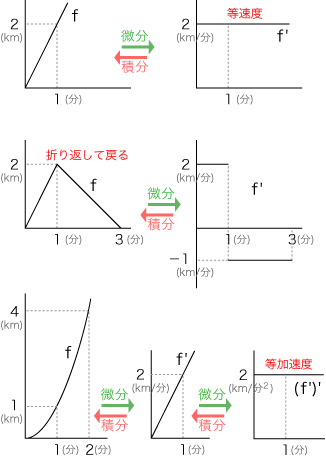
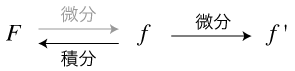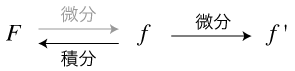- 関数の変化の仕方を求めるのが「微分」。逆に,変化の仕方からもとの関数を求めるのが「積分」。
- 関数 f に対し,f の変化を表現する関数 f' を求めること (その内容) を,「f を微分する」と言います。
また,これの逆のこととして,f が変化の表現となるような関数 F を求めること (その内容) を,「f を積分する」と言います。
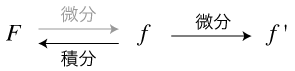
- f と f' (fの導関数) の例
- f : 直線道路を移動する自動車をつぎのように記述した関数:
- 直線上の1点Oを基準と定める。
時間の単位に「分」,距離の単位に「m」をそれぞれ選ぶ。
- 経過時間と基準点Oからの移動距離の対応を,分に対する数値と mに対する数値の対応に代える。──この対応 (関数) を f とする。
この f に対する f' はつぎの関係で定まる関数になる :
- 例えば,