ここに自動的に走る乗り物があって,A, B 二人が乗っている。
乗り物には,移動距離と速度を示すメータがそれぞれついている。
いま,ある時点で距離のメータと時計をリセットし,つぎのことを開始する:
A は,経過時間に対する距離を記録する
B は,経過時間に対する速度を記録する
一定時間が経過したところで,A と B は作業を終了する。
そして,A と B はそれぞれ記録をもとに「時間 - 距離」と「時間 - 速度」の2つのグラフを作成する。
|
「時間 - 距離」のグラフ(左) と「時間 - 速度」のグラフ(右):

このとき,実は,つぎのことが可能です:
- 「時間 - 距離」のグラフから「時間 - 速度」のグラフを得る
- 「時間 - 速度」のグラフから「時間 - 距離」のグラフを得る
そして,
「微分」: 「時間 - 距離」のグラフから「時間 - 速度」のグラフを得る操作
「積分」: 「時間 - 速度」のグラフから「時間 - 距離」のグラフを得る操作
|
ということになります (「微分・積分」の意味!)。
そこでこの操作ですが,考え方はつぎのようになります:
「小学生が算数で解ける形に変えよう (近似しよう)」
小学生はつぎのことができます:
- 経過時間に対し一定の割合で距離が増えるときの速度を求める。
- 速度が一定のときの走行距離を求める。
そこで,つぎのように近似してみます:
左のグラフを直線グラフに近似すると,この近似グラフには右の定値グラフが対応する。
右のグラフを定値グラフに近似すると,この近似グラフには左の直線グラフが対応する。
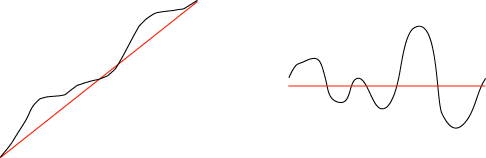
|
さらに,時間を区切って,近似 (直線と定値) をより精細にしてみます:
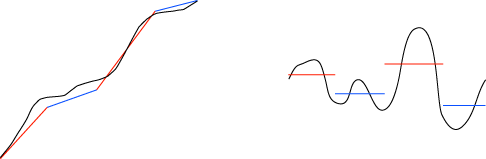

時間を細かく区切るほど近似は精密を増し,もとのグラフがほとんど再現されるようになります:
この例では,「時間 - 速度」の近似グラフからは「時間 - 距離」のグラフがほとんど再現されました。
しかし,「時間 - 距離」の近似グラフから「時間 - 速度」のグラフを再現するには,時間をさらに区分しなければなりません。

|
ここでは,「<時間-距離>対<時間-速度>」を使って「微分・積分」の概念を導入しましたが,「微分・積分」の意味を一般的に述べると,つぎのようになります:
「微分」: 「位置が変化する様」から「位置の変化率が変化する様」を得る操作
「積分」: 「位置の変化率が変化する様」から「位置が変化する様」を得る操作
|
|





