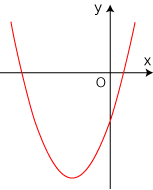
すなわち,値の代入を片っ端にやることは,関数を現すことになる。 逆に,式で記述されるタイプの関数は,方程式を呼ぶ。 すなわち,ある出力を導く入力を求めることは,方程式を現すことになる。 方程式の<代入値と式の値の領域>がユークリッド空間に埋め込めるものであるときには,この方程式に対応する関数グラフは,視覚化が可能になる。 通常扱う方程式は代入値と式の値が数であるが,それはこの条件にあてはまる。 ──1変数なら関数グラフは xy-座標平面に,2変数なら xyz-座標空間に,それぞれ視覚化できる。 一般に方程式は,<状態>のうちの一点をとらえた感じになっている。 そして,このときの<状態>が,関数にあたる。 方程式に<意味>を与える役回りを関数がしているわけであり,方程式と関数を対応させることは道理にあっている。 そして,関数グラフが視覚化できるとなれば,これは<状態>が視覚化されるということであるから,方程式がさらにとらえやすくなる。
|