Up 複数の立方体でなる図形の重心  

    「複数の正方形でなる図形の重心」の考えを「空間」に延長すれば，「複数の立方体でなる図形の重心」になります。

    同じ立方体 (「単位立方体」) がｎ個でなる立体図形Ｓを考えます。

    Ｓの重心をＧとし，各立方体の中心 (重心) をＰk とします (k＝1, ‥‥, ｎ)。
    各Ｐk には，同じ重力ベクトル F が作用しています。
    そこで，Gにおける「重力のモーメントが釣り合う」の条件は，つぎのようになります：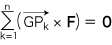
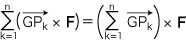
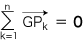
    そして外積の分配法則により
    となるので，つぎが導かれます：
    F は任意──すなわち，重力方向に対する図形の傾きは任意──なので，これは「重心」の条件になっていると見なせます。

    ここで，任意に ｘyz 直交座標を導入して， Ｇ(gx, gy, gz)， Ｐk(ｘk, ｙk, zk) (k＝1, ‥‥, n) とすれば，上の条件は，つぎのようになります：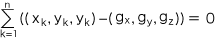
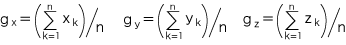
    すなわち，

    この式に，単位の立方体の体積 (数値) Δ をつぎのように組み入れます：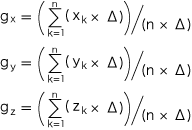


    これは，つぎの表現になります：