Up 渦巻きとフィボナッチ数 作成: 2014-07-16
更新: 2014-07-19

    つぎは，松ぼっくりの下から見た画像である：
    渦巻きが見えてくるので，その数を数えると，13。
    フィボナッチ数の一つである。
    また， (少し無理しつつも) つぎのような感じで，フラクタル構造を見ることができる：

    これを一例に，植物の形態形成では，フィボナッチ数を現すフラクタル性がいろいろ見出される(らしい)。
    そこで，「これはどうしたことか？」「フィボナッチ数にどんな秘密が？」となるわけである。


    しかしこの話題では，「秘密」はフィボナッチ数にではなく，黄金角にあるとしなければならない。
    実際，渦巻きなら，任意本数で描くことができる。
    「黄金角跳び回転」の中で出てきた「ｋ跳びでｎ個一巡」も，「ｎとｋが互いに素」が条件になることであって，フィボナッチ数に理由を求めることではない。
    つぎが「植物の形態形成とフィボナッチ数」の考え方になる：
      《黄金角の回転が先ずあり，これに「円形に配列する要素の大きさ」の制約が加わって，「ｋ跳びでｎ個一巡」のｎがフィボナッチ数になる。》


    黄金角の回転では，「ｋ跳びでｎ個一巡」の＜ｎ番目＞が回転の開始点にきて，かつ開始点と少しずれる。
    そこで，＜一段下げた円で同じプロセスを再開＞をフラクタル構造にすると，渦巻き模様が現れる。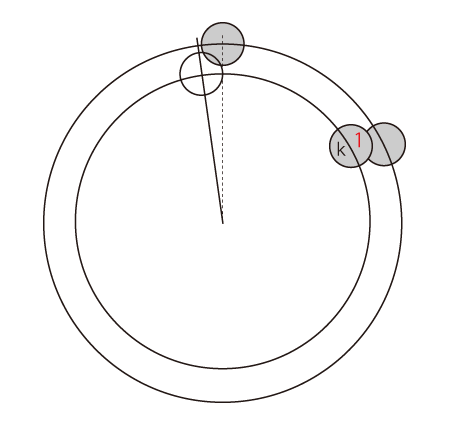
    また，この場合は，新しい配置が先の配置との隙間を埋めるふうになるので，密度の高いパックの実現になる。
    こうして，＜松ぼっくりを下から見た画像＞のようになる。