Up 黄金比の導出──正五角形から 作成: 2014-07-25
更新: 2014-07-25

    「正方形の，辺と対角線の長さの比は？」
    この問いから，√２が導かれてくる。
    「正五角形の，辺と対角線の長さの比は？」
    この問いから導かれてくるのが，黄金比φ (＝ (１＋√５)/2 ) である。

    (1) 黄金比の導出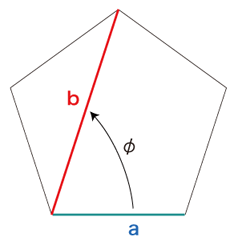
    黄金比φは，正五角形からつぎの長さの比として導出される：
    導出方法は，ユークリッド互除法である。

    先ず，ａは，つぎのようにｂの中に１回入って，ｒ1 余る：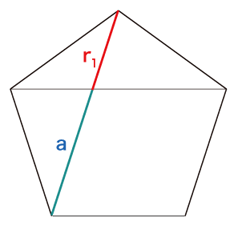

    　　　実際，図中の長さａが，つぎのように導かれる：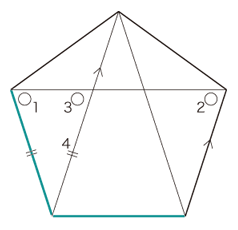

(番号は，推論の順序)

    ｒ1 は，つぎのようにａの中に１回入って，ｒ2 余る：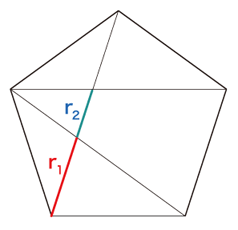

    ｒ1 は，つぎのようにとれる：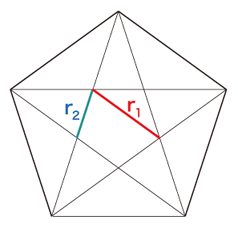

    　　　実際，図中の長さｒ1 が，つぎのように導かれる：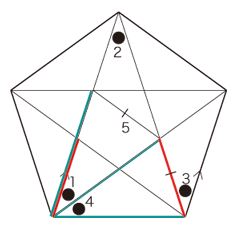

(番号は，推論の順序)

    小さい正五角形の中ｒ2 とｒ1 の位置関係は，もとの正五角形の中のａとｂの位置関係と同じである。
    よって，ユークリッド互除法の操作は，ここまでのプロセスと同型のプロセスを，延々と続けることになる。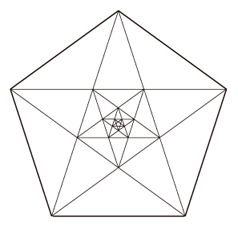

    すなわち，つぎのようになる：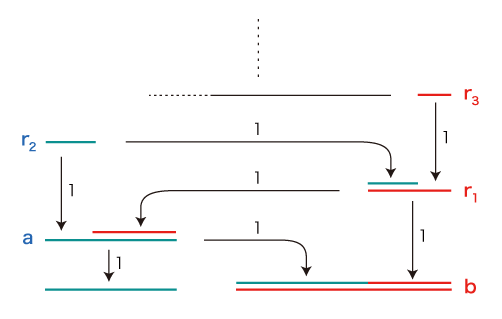

    そして，比の連分数表現が，つぎのように導かれる：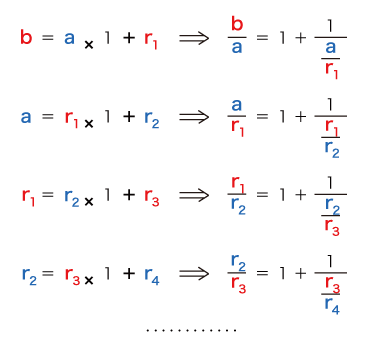



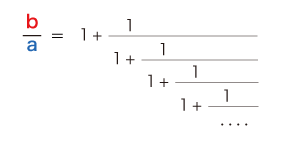
    (2) １＋φ＝φ2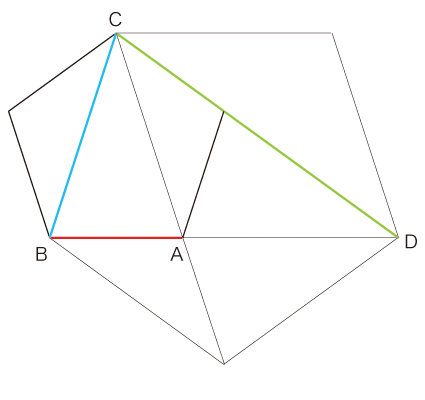
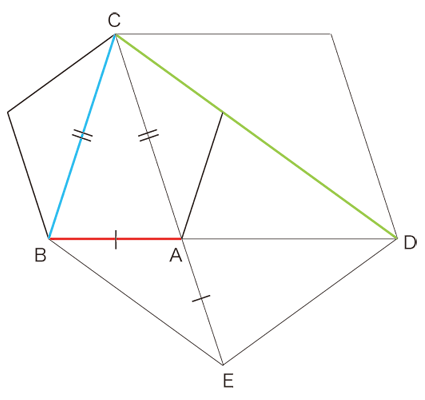
    φ2 を作図する──下図の AB に対する CD の比がφ2 である：
    この図から，１＋φ＝φ2 が導かれる：
    　　　実際，AB ＋ BC ＝ AE ＋ CA ＝ CE ＝ CD


    (3) 正五角形の作図
    １＋φ＝φ2 からは，φ＝ (１＋√５) / 2 を得る。
    そして φ＝ (１＋√５) / 2 を得ることで，正五角形の「コンパスと定木」による作図法を編み出せる。

    即ち，1，√５ (直角を夾む２辺の長さが 1と2の直角三角形の対辺の長さ), １＋√５, φ＝(１＋√５)/2 と順に作図して，つぎの２等辺三角形をつくる：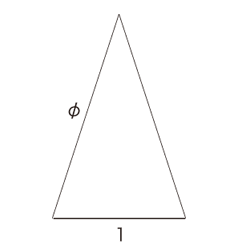
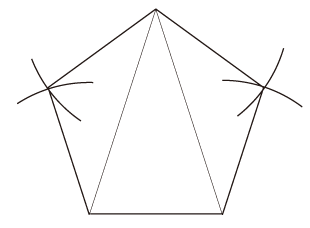
    そして，これから正五角形ができる：