学校数学の中では,「対称」な平面図形として,点対称形,線対称形の他に,もうひとつの「対称形」が登場します──ただし,明示的には「対称形」として扱われませんが。それは,つぎのように定義される形です。
図形X は,つぎの条件を満たす点 O と 360 の約数 n > 2, < 360 が存在するとき,「回転対称形」と呼ぶ:
O を回転の中心とする 360/n 度の回転で,X は自分自身に重なる
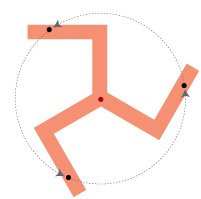
ここで,「回転対称形」の用語はここだけのものです。これといった用語が既存のものにないので,この語を作りました。
| 註 : |
「n > 2」とした意味は:
n=1 では,任意の図形X が条件を満たすことになる。
n=2 の場合は,「鏡が点の鏡対称 (点対称)」の見方に譲る。
|
|

