形F1 から形F2 への変形は,つぎが内容になっている:
翻って,「同形」は,二つの図形の点対応 (関数) で表現されるものである。 例:つぎの二つの形は,同形である: 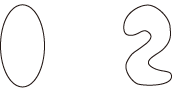
──「同形」の点対応は,つぎのfのようになる: 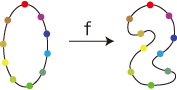
つぎは,同形でない: 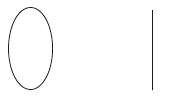
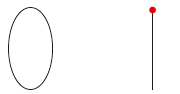
つぎも,同形でない: 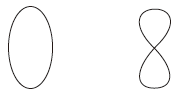
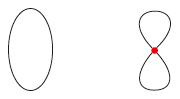
|
| Up | 「同形」の点対応 | 更新: 2015-12-17 |
形F1 から形F2 への変形は,つぎが内容になっている:
翻って,「同形」は,二つの図形の点対応 (関数) で表現されるものである。 例:つぎの二つの形は,同形である: 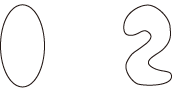
──「同形」の点対応は,つぎのfのようになる: 
つぎは,同形でない: 

つぎも,同形でない: 

|