
ひとは上の2つの閉曲面──球面とトーラス──を,タイプの違うものとして観る。 ホモロジー加群は,ひとのこの直観に数学的表現/裏付けを与えようとする探求の中から,出て来たものである。 翻って,ホモロジー加群は何をするものかというと,閉曲面の分類をするものである。 数学は推理の自動機械である。 ホモロジー加群を使った閉曲面の探求が開始されると,ひとの直観が及ばなかったものを示してくるようになる。 ひとはこれを「本質」と呼ぶ。
数学と疎遠でいるのは,もったいないことなのである。 さて,閉曲面の本質的違いを捉えようとするホモロジー加群の方法は,どのようなものか? トーラスには穴がある。 これが球面との決定的違いになっている。 では,穴とは何か? 数学に感心してしまうのは,これにきっちり表現を与えてしまうことである。 曲面の上で一回りしてみる。 球面の場合,一周経路には内と外ができる。 トーラスでは,内と外ができる経路のほかに,内と外ができない経路が2通りとれる: 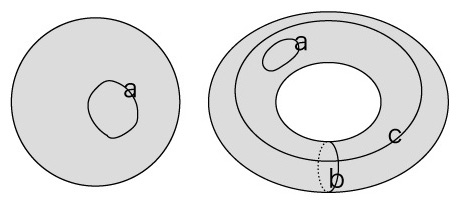
そこで,タイプの違う経路を数学的に表現できればよさそうだ,となる。 一周経路を「サイクル」と呼ぶことにする。 内と外ができるサイクルを,面のバウンダリ (境界) になるサイクルと捉える。 タイプaのサイクルはバウンダリサイクルで,タイプb,cのサイクルはバウンダリサイクルではない。 こうして,サイクルの中にバウンダリサイクルがあるかどうか,あればそれはいくつのタイプに分かれるかで,閉曲面の分類ができそうな感じになってきた。 しかしまだ雲をつかむような感じである。 雲をつかむような感じなのは,サイクルが定まらないためである。 例えば,つぎのbとb′,cとc′ は,それぞれ同じ扱いになるはずのものなので,1つにしなければならない。 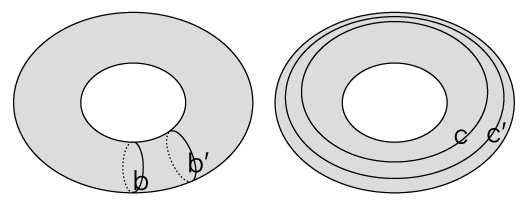
といった問題を解決していって,ホモロジー加群の発明に至る。 ホモロジー加群は,「サイクルの中にバウンダリサイクルがあるかどうか,あればそれはいくつのタイプに分かれるか」が,これを見ればわかるしくみになっている。 |