閉曲面の三角形分割は,閉曲面上の経路を三角形複体上のチェインに表現しようとするものである。
経路は,辺の組で表現できるはずである。
ほんとに?
チェインでは,「通った辺を後から逆方向に通る」が要所になる。
チェインの縮約になったり,サイクルを分離することになるからである。
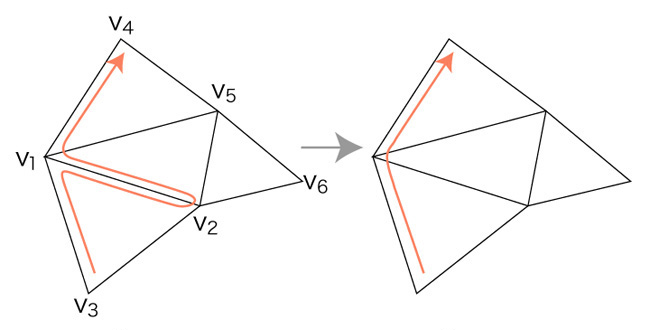
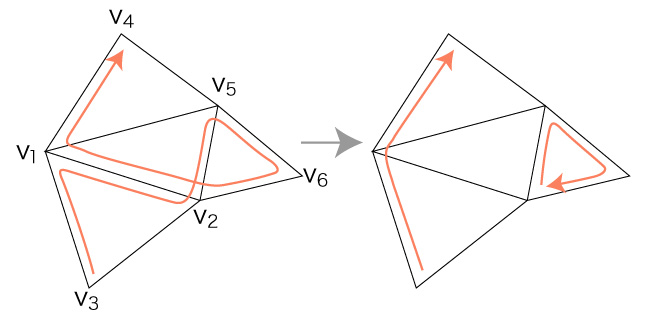
チェインの表現は,このキャンセルを表現するものになっていなければならない。
辺の組だけなら,チェインの中に同じ辺が2つあるとき,それがキャンセルになるのかそうでないのかがわからない。
では,どうしたらよい?
有向辺の組にする。
さらに,つぎのようにすると,チェインの表現を短縮したり,チェインの縮約を代数的に計算することが,できるようになる:
- 有向辺の組を,有向辺の和の形に表す。
- \( \overrightarrow{v_j v_k}\ \) の逆 \( \ \overrightarrow{v_k v_j}\ \) を \( - \overrightarrow{v_j v_k}\ \) で表す。’
- 有向辺 \( \overrightarrow{v_i v_j}\ \) の \( n \) 個の和を,\( n\ \overrightarrow{v_i v_j}\ \) で表す。
\( n\ ( - \overrightarrow{v_i v_j}\ ) \) を \( ( - n )\ \overrightarrow{v_i v_j}\ \) と書く。

|
\[
\begin{align}
& \overrightarrow{v_3 v_1}\ + \overrightarrow{v_1 v_2}\ +
\overrightarrow{v_2 v_5}\ + \overrightarrow{v_5 v_6}\ + \overrightarrow{v_6 v_2}\ +
\overrightarrow{v_2 v_1}\ + \overrightarrow{v_1 v_4} \\
=
& ( \overrightarrow{v_3 v_1}\ + \overrightarrow{v_1 v_4}\ )
+ ( \overrightarrow{v_1 v_2}\ + \overrightarrow{v_2 v_1}\ )
+ ( \overrightarrow{v_2 v_5}\ + \overrightarrow{v_5 v_6}\ + \overrightarrow{v_6 v_2}] ) \\
=
& ( \overrightarrow{v_3 v_1}\ + \overrightarrow{v_1 v_4}\ )
+ ( \overrightarrow{v_1 v_2}\ + ( - \overrightarrow{v_1 v_1} ) )
+ ( \overrightarrow{v_2 v_5}\ + \overrightarrow{v_5 v_6}\ + \overrightarrow{v_6 v_2}] ) \\
=
& ( \overrightarrow{v_3 v_1}\ + \overrightarrow{v_1 v_4}\ )
+ ( \overrightarrow{v_2 v_5}\ + \overrightarrow{v_5 v_6}\ + \overrightarrow{v_6 v_2}] )
\end{align}
\]
|
了解?
数学科の学生は,了解してしまう。
中学数学以来,「逆は\( - \) 」「合わせるは \( + \) 」に馴らされてきているからである。
ここは,「この \( -, + \) は何?」と問うところである。
\( -, + \) の導入は,つぎのことをしたのである:
「有向辺で生成される \( \mathbb{Z} \) 加群を導入」
導入した \( \mathbb{Z} \) 加群を,1次チェイン加群と呼び,\( C_1 \) と表記する。
「1次」のことばと添え数「1」は辺の幾何学的次元1を指しているが,これをことさら記すのは,この後に
0次チェイン加群 \( C_0 \)
2次チェイン加群 \( C_2 \)
を導入することになるからである。
\( C_1 \) の要素を,改めて「チェイン」と呼ぶ。
これまでは「辺の連結」がチェインのイメージだったが,ここからのチェインはこれではないことに注意。
例えば,チェイン \( \overrightarrow{v_1 v_2}\ + \overrightarrow{v_3 v_4}\ \) は,辺の連結ではない。
辺を並べただけのチェインにどんな意味がある?
心配は無用。
辺を並べただけのチェインに,意味は求めない。
実際に扱うことになるのは,サイクル──辺を連結して一周──である。
しかし,サイクルの定位や計算をしようとすると,領域がチェーンまで拡がる。
「辺を並べただけのチェーン」の導入となるのは,このためである,
|


