Up バウンダリサイクル──\( \mathbb{Z} \)加群 \( C_2 \) の導入 作成: 2023-10-10
更新: 2023-10-10

    トーラスには，球面には無い周回のタイプを見て取れる：
    \( a \) のタイプはどの閉曲面にもあり，これは「面の境界になっている」で特徴づけられる。

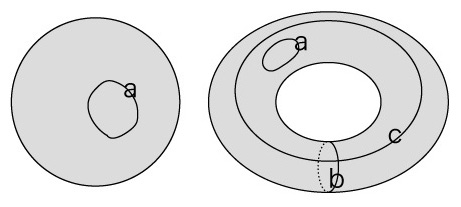
    閉曲面における「周回が面の境界になっているかどうか」は，三角面複体では「サイクルが面の境界になっているかどうか」になる。
    面の境界になっているサイクルを，バウンダリサイクルと呼ぶ。
    「周回が面の境界になっているかどうか」は，ここに「サイクルがバウンダリサイクルかどうか」の表現を得る。


    さて，サイクルがバウンダリサイクルかどうかは，面の表現ができてからの話である。
    面は，辺を共有する三角形のつくる面である。
    この面は，有向面にする必要がある。
    サイクルが，\( \mathbb{Z} \) 加群 \( C_1 \) の要素として，有向だからである。

    有向面を，頂点をたどる順番で表そう。
    つぎのように：
    \[ ( v_3 v_2 ) ( v_2 v_5 ) ( v_5 v_1 ) ( v_1 v_3 )\ \ \bigl(\ = ( v_1 v_3 ) ( v_3 v_2 ) ( v_2 v_5 ) ( v_5 v_1 ) \\ = ( v_5 v_1 ) ( v_1 v_3 ) ( v_3 v_2 ) ( v_2 v_5 )\ = ( v_2 v_5 ) ( v_5 v_1 ) ( v_1 v_3 ) ( v_3 v_2 )\ \ \bigr) \]
    これを有向三角面の和に見るために，有向面の加法を「共有する辺のキャンセル」として導入する：
      \[ \begin{align} & ( v_3 v_2 ) \color{red}{ ( v_2 v_1 ) } ( v_1 v_3 )\ + \color{red}{ ( v_1 v_2 ) } ( v_2 v_5 ) ( v_5 v_1 ) \\ =\ & ( v_1 v_3 ) ( v_3 v_2 ) \color{red}{ ( v_2 v_1 ) }\ + \color{red}{ ( v_1 v_2 ) } ( v_2 v_5 ) ( v_5 v_1 ) \\ =\ & ( v_1 v_3 ) ( v_3 v_2 ) ( v_2 v_5 ) ( v_5 v_1 ) \\ \end{align} \] \[ ( v_3 v_2 ) ( v_2 v_1 ) ( v_1 v_3 )\ \ = -\ ( v_3 v_1 ) ( v_1 v_2 ) ( v_2 v_3 ) \\ \]

    上の \( +, - \) の導入は，つぎを含蓄している：
      「有向面で生成される \( \mathbb{Z} \) 加群を導入」

    導入した \( \mathbb{Z} \) 加群を，２次チェイン加群と呼び，\( C_2 \) と表記する。
    「２次」のことばと添え数「２」は，面の幾何学的次元２を指す。