閉曲面を分類したくなるのは,つぎの二つの閉曲面──球面とトーラス──を見せられると,これを区別したい衝動が沸々と沸き上がるからである^^; 
では,どんなことばを用いて区別するか? 「トーラスには,球面には無い穴がある」? しかしこれには,「穴って何よ」が返ってくる。 実際,問題は「穴」を特徴づけることばである。 ここで,「穴」を特徴づけることばを「閉曲面上の周回のタイプ」とする。 トーラスには,球面には無い周回のタイプを見て取れるからである: 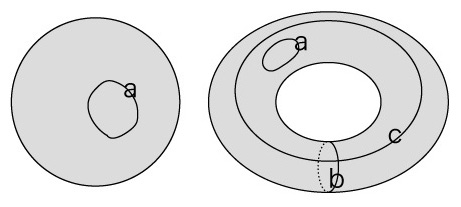
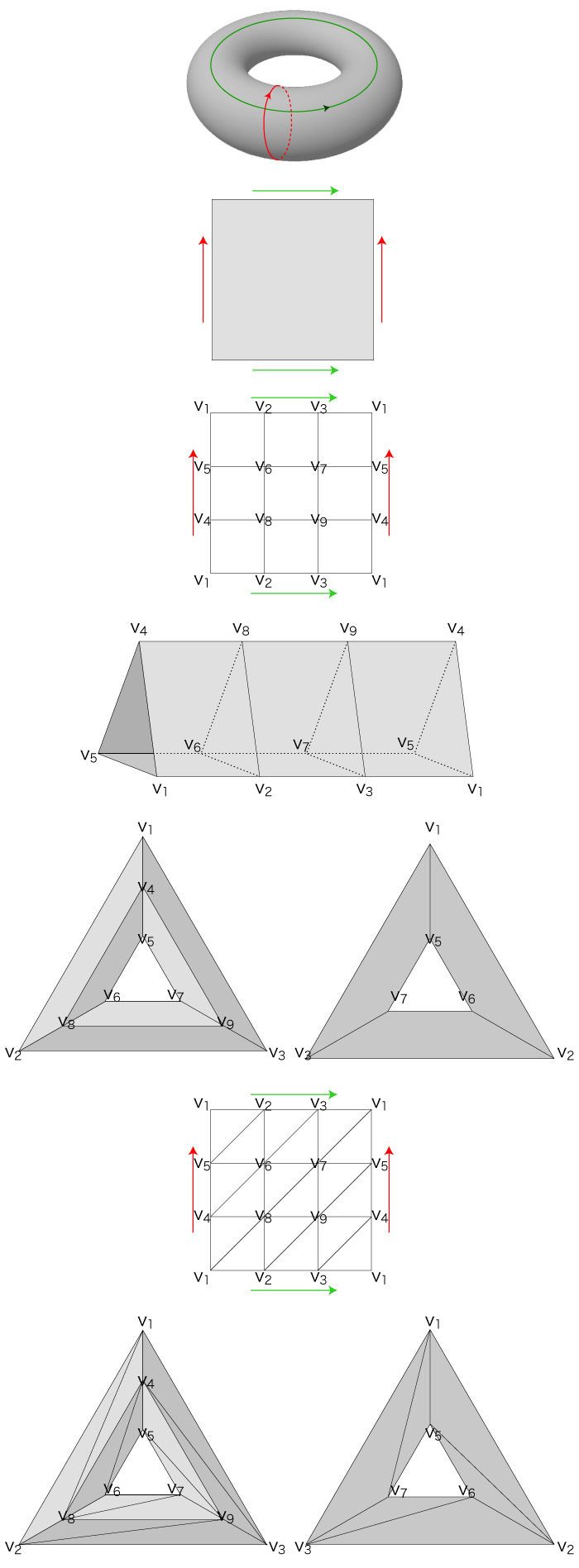
しかし,このタイプを述べる仕方──集合・構造のことばを用いて述べる仕方──が,定まらない。 { 周回 } が無限集合になることも,これの一因。 「周回のタイプに着目した閉曲面の特徴づけ」は雲を摑むような話になる。 さて,どうするか? アイデアは「三角形分割」──閉曲面を三角形複体に変換: 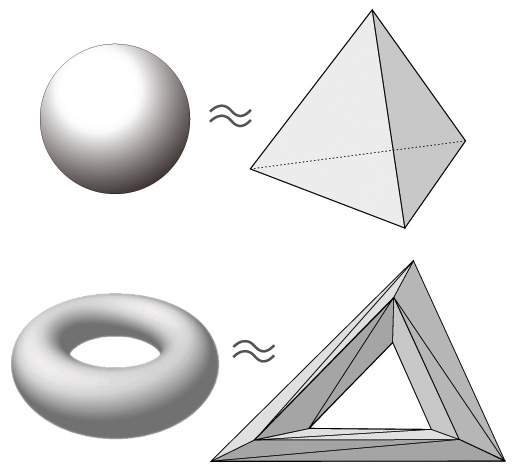
この変換の意図は,閉曲面上の経路を,三角形複体上の辺の組──「チェイン」──に変換することである。 閉曲面上の周回は無限にあるが,<三角形の辺を伝って周回>──「サイクル」──なら有限である。 そして有限なら,「虱潰し」の方法がとれる。 「周回のタイプに着目した閉曲面の特徴づけ」は,もう雲を摑むような話でなくなる。 |