Up

トーラスのホモロジー加群 \( H_1 \) の基底

作成: 2023-10-13 更新: 2023-10-13

---

\( C_1, C_2 \) の基底を，つぎのように定めた：

\( \partial_2 \) の表現行列の計算から，18 個の \( \partial_2 f_k \) のうち \( \partial_2 f_{15} \) を除く 17 個が， \( Im( \partial_2 ) \) の基底を成すことが導かれた： \[ \partial_2 f_{1} = e_{1} + e_{5} + e_{7} \\ \partial_2 f_{2} = e_{2} + e_{6} + e_{8} \\ \partial_2 f_{3} = e_{3} + e_{4} + e_{9} \\ \partial_2 f_{4} = e_{4} + e_{10} + e_{7} \\ \partial_2 f_{5} = e_{5} + e_{11} + e_{8} \\ \partial_2 f_{6} = e_{6} + e_{12} + e_{9} \\ \partial_2 f_{7} = e_{10} + e_{14} + e_{16} \\ \partial_2 f_{8} = e_{11} + e_{15} + e_{17} \\ \partial_2 f_{9} = e_{12} + e_{13} + e_{18} \\ \partial_2 f_{10} = e_{13} + e_{19} + e_{16} \\ \partial_2 f_{11} = e_{14} + e_{20} + e_{17} \\ \partial_2 f_{12} = e_{15} + e_{21} + e_{18} \\ \partial_2 f_{13} = e_{19} + e_{23} + e_{25} \\ \partial_2 f_{14} = e_{20} + e_{24} + e_{26} \\ \partial_2 f_{16} = e_{22} + e_{1} + e_{25} \\ \partial_2 f_{17} = e_{23} + e_{2} + e_{26} \\ \partial_2 f_{18} = e_{24} + e_{3} + e_{27} \\ \] また，\( \partial_1 \) の表現行列の計算から，つぎの 19 個のサイクルが \( Ker( \partial_1 ) \) の基底を成すことが導かれた：：

\( c_1 = e_{1} + e_{5} + e_{7} \)	\( c_2 = e_{2} + e_{6} + e_{8} \)	\( c_3 = e_{3} + e_{4} + e_{9} \)
\( c_4 = e_{1} + e_{25} + e_{22} \)	\( c_5 = e_{2} + e_{26} + e_{23} \)	\( c_6 = e_{3} +e_{27} + e_{24} \)
\( c_7 = - e_{1} + e_{4} + e_{10} - e_{5} \)	\( c_8 = - e_{2} + e_{5} + e_{11} - e_{6} \)	\( c_9 = - e_{3} + e_{6} + e_{12} - e_{4} \)
\( c_{10} = - e_{3} + e_{26} + e_{20} - e_{27} \)	\( c_{11} = e_{27} + e_{21} + e_{22} \)
\( c_{12} = e_{1} + e_{2} + e_{3} \)	\( c_{13} = e_{3} - e_{22} + e_{19} - e_{26} \)
\( c_{14} = e_{4} + e_{13} + e_{22} \)	\( c_{15} = e_{2} + e_{26} - e_{14} - e_{5} \)	\( c_{16} = e_{3} - e_{22} + e_{18} - e_6 \)
\( c_{17} = - e_{3} + e_{26} + e_{16} - e_{4} \)	\( c_{18} = - e_{1} + e_{27} + e_{17} - e_{5} \)	\( c_{19} = e_{27} - e_{15} - e_{6} - e_{2} - e_{1} \)

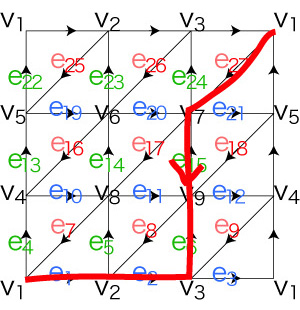\( c_{1} \) 〜 \( c_{11} \) は，バウンダリサイクルであり，\( Im( \partial_2 ) \) に属する。 \( c_{12}, c_{13} \) は，同じ同値類に属する： \[ \begin{align} & c_{12} - c_{13} \\ =\ & ( e_{1} + e_{2} + e_{3} ) - ( e_{3} - e_{22} + e_{19} - e_{26} ) \\ =\ & e_{1} + e_{2} + e_{26} - e_{19} + e_{22} \\ =\ & ( e_{1} + e_{25} + e_{22} ) + ( e_{2} + e_{26} + e_{23} ) - ( e_{19} + e_{23} + e_{25} ) \\ =\ & \partial_2 f_{16} + \partial_2 f_{17} - \partial_2 f_{13} \\ & \in Im( \partial_2 ) \end{align} \]

\( - c_{14}, c_{15}, c_{16} \) は，同じ同値類に属する： \[ \begin{align} & c_{15} - ( - c_{14} ) \\ =\ & c_{14} + e_{2} + c_{15} - e_{2} \\ & \in Im( \partial_2 ) \end{align} \]

\( c_{17}, c_{18}, c_{19} \) は，同値類 \( - [ c_{12} ] - [ c_{14} ] \) に属する。 実際，いずれも \( - c_{12} - c_{14} \) と同値になる。

\( H_1 = Ker( \partial_1 ) / Im( \partial_2 ) \) は，次元が 19 - 17 = 2。 よって，２つの同値類 \( [ c_{12} ],\ [ c_{14} ] \) は，\( H_1 \) の基底になる。 特に，この２つの同値類が，「バウンダリサイクルでないサイクル」のタイプ──異なる２タイプ──を表現していることになる。