Up

\( \partial_1 \) の表現行列

作成: 2023-10-12 更新: 2023-10-12

---

\( C_1 \) の基底を，つぎのように定めた：

\( C_0 \) の基底は，\( \{ v_1, v_2, v_3, v_4, v_5, v_6, v_7, v_8, v_9 \} \) をとる。 各 \( e_i \) のバウンダリは， \[ \partial_1 e_1 = v_2 - v_1 \\ \partial_1 e_2 = v_3 - v_2 \\ \partial_1 e_3 = v_1 - v_3 \\ \ \\ \partial_1 e_4 = v_4 - v_1 \\ \partial_1 e_5 = v_8 - v_2 \\ \partial_1 e_6 = v_9 - v_3 \\ \ \\ \partial_1 e_7 = v_1 - v_8 \\ \partial_1 e_8 = v_2 - v_9 \\ \partial_1 e_9 = v_3 - v_4 \\ \] \[ \partial_1 e_{10} = v_8 - v_4 \\ \partial_1 e_{11} = v_9 - v_8 \\ \partial_1 e_{12} = v_4 - v_9 \\ \ \\ \partial_1 e_{13} = v_5 - v_4 \\ \partial_1 e_{14} = v_6 - v_8 \\ \partial_1 e_{15} = v_7 - v_9 \\ \ \\ \partial_1 e_{16} = v_4 - v_6 \\ \partial_1 e_{17} = v_8 - v_7 \\ \partial_1 e_{18} = v_9 - v_5 \\ \] \[ \partial_1 e_{19} = v_6 - v_5 \\ \partial_1 e_{20} = v_7 - v_6 \\ \partial_1 e_{21} = v_5 - v_7 \\ \ \\ \partial_1 e_{22} = v_1 - v_5 \\ \partial_1 e_{23} = v_2 - v_6 \\ \partial_1 e_{24} = v_3 - v_7 \\ \ \\ \partial_1 e_{25} = v_5 - v_2 \\ \partial_1 e_{26} = v_6 - v_3 \\ \partial_1 e_{27} = v_7 - v_1 ] \] よって，基底 \( \{ e_i \}, \{ v_j \} \) に対する \( \partial_1 : C_1 \rightarrow C_0 \) の表現行列は， 以下，基底 \( \{ e_i \} \) の変換によってこの行列の階数を減らす作業をする。 行列の操作において考えることは，どの \( e_i \) を変更せずに残すかである。

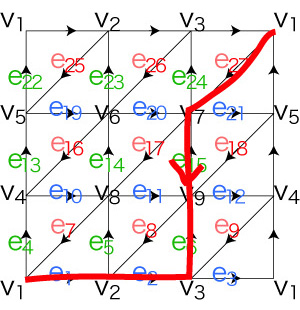
図に見て取れるように，各有向辺のバウンダリ (両端の頂点) は，つぎの８個の有向辺がつくるチェインのバウンダリに表現できる： \[ e_1, e_2, e_4, e_5, e_6, e_{13}, e_{14}, e_{15} \] これらを，「変更せずに残す \( e_i \) 」とする。 \( e'_8 = e_8 + e_6 \) \( e'_{11} = e_{11} - e_6 \) \( e'_{12} = e_{12} + e_6\) \( e'_{18} = e_{18} - e_6 \) \( e'_7 = e_7 + e_5 \) \( e'_{10} = e_{10} - e_5 \) \( e''_{11} = e'_{11} + e_5 \) \( e'_{17} = e_{17} - e_5 \) \( e''_{17} = e'_{17} + e_{27} \) \( e'_{20} = e_{20} - e_{27} \) \( e'_{21} = e_{21} + e_{27} \) \( e'_{24} = e_{24} + e_{27} \) \( e'_{16} = e_{16} + e_{26} \) \( e'_{19} = e_{19} - e_{26} \) \( e''_{20} = e'_{20} + e_{26} \) \( e'_{23} = e_{23} + e_{26} \) \( e''_{18} = e'_{18} - e_{22} \) \( e'_{19} = e_{19} - e_{22} \) \( e'_{21} = e_{21} + e_{22} \) \( e'_{25} = e_{25} + e_{22} \) \( e'_{9} = e_{9} + e_{4} \) \( e''_{10} = e'_{10} + e_{4} \) \( e''_{12} = e'_{12} - e_{4} \) \( e'_{16} = e_{16} - e_{4} \) \( e''_{7} = e'_{7} + e_{1} \) \( e'''_{10} = e''_{10} - e_{1} \) \( e'''_{17} = e''_{17} - e_{1} \) \( e''_{25} = e'_{25} + e_{1} \) \( e''_{8} = e'_{8} + e_{2} \) \( e'''_{11} = e''_{11} - e_{2} \) \( e''_{23} = e'_{23} + e_{2} \) \( e''_{9} = e'_{9} + e_{3} \) \( e'''_{12} = e''_{12} - e_{3} \) \( e'''_{16} = e''_{16} - e_{3} \) \( e'''_{18} = e''_{18} + e_{3} \) \( e'''_{19} = e''_{19} + e_{3} \) \( e'''_{20} = e''_{20} - e_{3} \) \( e''_{24} = e'_{24} + e_{3} \) \( e'_{3} = e_{3} + ( e_{1} + e_{2} ) \) \( e'_{22} = e_{22} + ( e_{4} + e_{13} ) \) \( e'_{26} = e_{26} + ( e_{2} - e_{5} - e_{14} ) \) \( e'_{27} = e_{27} - ( e_{1} + e_{2} + e_{6} + e_{15} ) \) 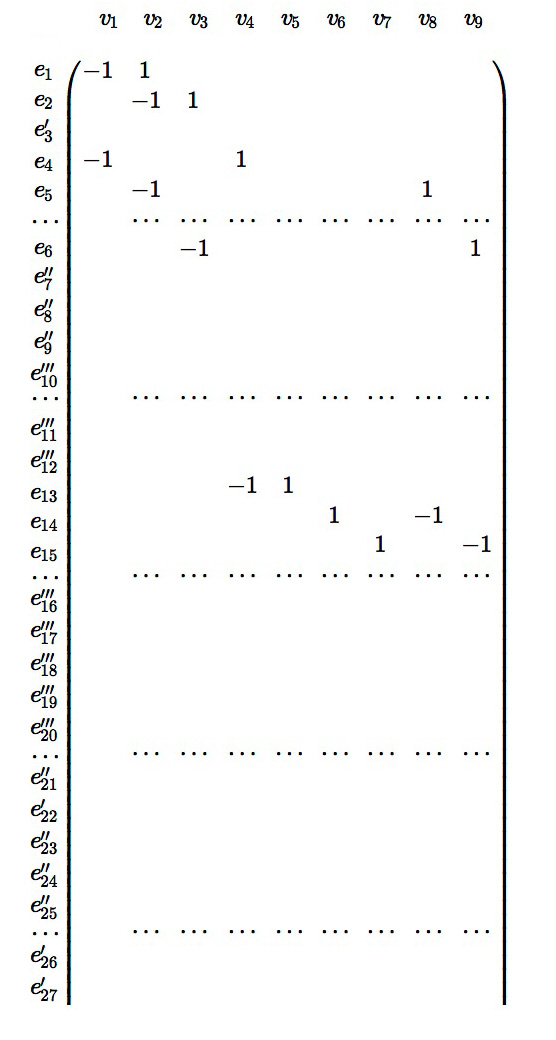この行列は，つぎのことを示している： 写像 \( \partial_1 \) では，27次元が８次元になり，19次元が潰れる。 即ち，\( Ker( \partial_1 ) \) が 19次元，\( Ker( \partial_1 ) \) の補空間が ８次元。 実際，つぎのチェインが，補空間の基底を成す： \[ e_1,\ e_2,\ e_4,\ e_5,\ e_6,\ e_{13},\ e_{14},\ e_{15}, \\ \] そして，つぎのサイクルが，\( Ker( \partial_1 ) \) の基底を成す： \[ e'_{3} = e_{3} + ( e_{1} + e_{2} ) = e_{1} + e_{2} + e_{3} \] \[ e''_{7} = e'_{7} + e_{1} = ( e_7 + e_5 ) + e_{1} = e_{1} + e_5 + e_7 \] \[ e''_{8} = e'_{8} + e_{2} = ( e_8 + e_6 ) + e_{2} = e_{2} + e_6 + e_8 \] \[ e''_{9} = e'_{9} + e_{3} = ( e_{9} + e_{4} ) + e_{3} = e_{3} + e_{4} + e_{9} \] \[ e'''_{10} = e''_{10} - e_{1} = ( e'_{10} + e_{4} ) - e_{1} = ( ( e_{10} - e_5 ) + e_{4} ) - e_{1} \\ = e_{4} + e_{10} - e_5 - e_{1} \] \[ e'''_{11} = e''_{11} - e_{2} = ( e'_{11} + e_5 ) - e_{2} = ( ( e_{11} - e_6 ) + e_5 ) - e_{2} \\ = e_5 + e_{11} - e_6 - e_{2} \] \[ e'''_{12} = e''_{12} - e_{3} = ( e'_{12} - e_{4} ) - e_{3} = ( ( e_{12} + e_6 ) - e_{4} ) - e_{3} \\ = e_6 + e_{12} - e_{4} - e_{3} \] \[ e'''_{16} = e''_{16} - e_{3} = ( e'_{16} - e_{4} ) - e_{3} = ( ( e_{16} + e_{26} ) - e_{4} ) - e_{3} \\ = - e_{3} + e_{26} + e_{16} - e_{4} \] \[ e'''_{17} = e''_{17} - e_{1} = ( e'_{17} + e_{27} ) - e_{1} = ( ( e_{17} - e_{5} ) + e_{27} - e_{1} \\ = e_{27} + e_{17} - e_{5} - e_{1} \] \[ e'''_{18} = e''_{18} + e_{3} = ( e'_{18} - e_{22} ) + e_{3} = ( ( e_{18} - e_6 ) - e_{22} ) + e_{3} \\ = e_{3} - e_{22} + e_{18} - e_6 \] \[ e'''_{19} = e''_{19} + e_{3} = ( e'_{19} - e_{22} ) + e_{3} = ( ( e_{19} - e_{26} ) - e_{22} ) + e_{3} \\ = - e_{22} + e_{19} - e_{26} + e_{3} \] \[ e'''_{20} = e''_{20} - e_{3} = ( e'_{20} + e_{26} ) - e_{3} = ( ( e_{20} - e_{27} ) + e_{26} ) - e_{3} \\ = e_{26} + e_{20} - e_{27} - e_{3} \] \[ e''_{21} = e'_{21} + e_{22} = ( e_{21} + e_{27} ) + e_{22} = e_{27} + e_{21} + e_{22} \] \[ e'_{22} = e_{22} + ( e_{4} + e_{13} ) = e_{4} + e_{13} + e_{22} \] \[ e''_{23} = e'_{23} + e_{26} = ( e_{23} + e_{2} ) + e_{26} = e_{23} + e_{26} + e_{2} \] \[ e''_{24} = e'_{24} + e_{3} = ( e_{24} + e_{27} ) + e_{3} = e_{27} + e_{24} + e_{3} \] \[ e''_{25} = e'_{25} + e_{1} = ( e_{25} + e_{22} ) + e_{1} = e_{25} + e_{22} + e_{1} \] \[ e'_{26} = e_{26} + ( e_{2} - e_{5} - e_{14} ) = e_{26} - e_{14} - e_{5} + e_{2} \] \[ e'_{27} = e_{27} - ( e_{1} + e_{2} + e_{6} + e_{15} ) = e_{27} - e_{15} - e_{6} - e_{2} - e_{1} \]