線型空間 \(U,\, V\) のテンソル積 \(U \otimes V\) を考える。
\(U,\, V\) の基底
\[
\{ {\bf u}_1, \cdots, {\bf u}_m \} \\
\{ {\bf v}_1, \cdots, {\bf v}_n \}
\]
に対するつぎの集合は,\(U \otimes V\) の基底になる:
\[
\{ {\bf u}_i \otimes {\bf v}_j \,|\, i = 1, \cdots, m; \, j = 1,\cdots, n \}
\]
\(U \otimes V\) から線型空間 \(W\) への線型写像
\[
f : U \otimes V \longrightarrow W
\]
の表現行列 \(A\) は,つぎのようになっている:
- \((m \times n)\) 個の \( {\bf u}_i \otimes {\bf v}_j\) を,1列に並べる。
- この配列に対する \( {\bf x} \in U \otimes V\) の座標を,\( (x^1, \cdots, x^{m \times n})\) とする。
- \(A\) の \(k\) 行が \((a^k_1, \cdots, a^k_{m \times n})\) であるとは, \(f(\bf x)\) の \({\bf w}_k\) 成分が
\[
a^k_1 x^1 + \cdots + a^k_{m \times n} x^{m \times n}
\]
になるということ。
ここで,「1列に並べる」を「行列に並べる」に変える:
- \((m \times n)\) 個の \({\bf u}_i \otimes {\bf v}_j\) を,つぎのように配列する:
\[\left(
\begin{array}{ccc}
{\bf u}_1 \otimes {\bf v}_1 & \cdots & {\bf u}_1 \otimes {\bf v}_n \\
& \cdots & \\
{\bf u}_m \otimes {\bf v}_1 & \cdots & {\bf u}_m \otimes {\bf v}_n \\
\end{array}
\right)
\]
- \( \bf x\) の座標を,基底の配列と対応させてつぎのように配列する:
\[\left(
\begin{array}{ccc}
x^{11} & \cdots & x^{1n} \\
& \cdots & \\
x^{m1} & \cdots & x^{mn} \\
\end{array}
\right)
\]
- \(A\) の \(k\) 行の項を,つぎのように行列の形に配列する:
\( a^k_t\) と積をなすのが \(x^{ij} \) であるとき:
\( a^k_t\) を,\( a^k_{ij}\) として,行列の \((i, j) \) の場所の置く
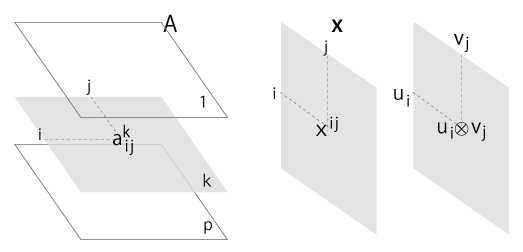
こうして,\(f\) は,立方配列の形に表現されることになる。
いまは2つの線型空間のテンソル積であるが,これが3つ以上になると,この表現──「超行列」と呼んでおく──は無理となる。
|

