偽テンソルには,「添字がついているから,テンソルだ」タイプのものがある。
「εテンソル」は,それである。
\(\epsilon_{i\,j\,k}\) が,つぎのように定義される:
\[
\epsilon_{i\,j\,k} =
\begin{cases}
+1 & (\ ( i, j, k)\ が偶順列\ ) \\
-1 & ( \ ( i, j, k)\ が奇順列\ ) \\
0 & (\ i, j, k\ のうち等しいものがある\ )
\end{cases}
\]
「添字がついているからテンソルだ」の思いは,,
である。
「\(\epsilon\) テンソル」の \(\epsilon_{i\,j\,k}\) は,つぎの立方超行列の中に配置できる:
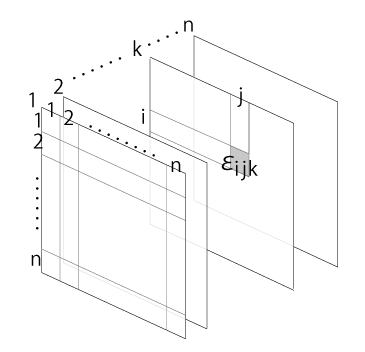
数学のテンソルは,「線型代数」の中の概念である。
εは,そうではない。
「εテンソル」は,偽テンソルである。
εを「テンソル」に仕立てようとすれば,「集合」のカテゴリーでこれをやることになる。
この方法を示しておく。
簡単のために,\( i, j, k \in \{ 1, 2, 3 \} \) の場合で説明する。
集合 \(\{ 1, 2, 3 \}\) を \(N\) , とおく。
そして,写像
\[
\epsilon : N \times N \times N \longrightarrow \{ +1, -1, 0 \}
\]
をつぎのように定義する:
\[
\epsilon (i\,j\,k) =
\begin{cases}
+1 & (\ ( i, j, k)\ が偶順列\ ) \\
-1 & ( \ ( i, j, k)\ が奇順列\ ) \\
0 & (\ i, j, k\ のうち等しいものがある\ )
\end{cases}
\]
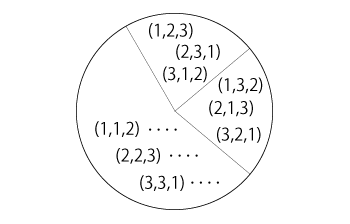
\( N \times N \times N \) 上の同値関係
\[
( i, j, k) \sim ( i', j', k')
\]
を
\[
\epsilon( i, j, k) = \epsilon( i', j', k')
\]
で定義し,この同値関係で \( N \times N \times N \) を類別した商集合を,\( N \otimes N \otimes N \) で表す。
──テンソル記号「\(\otimes\)」のこの使用は,もちろん無理矢理である。
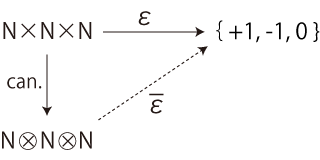
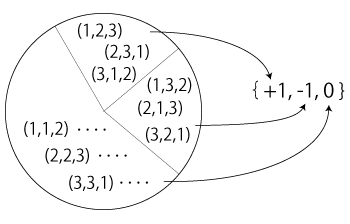
\( \bar{\epsilon} \) は,1対1対応であり, 「集合」のカテゴリーでの「同型 isomorphism」である。
|



