「テンソル」は「ベクトル」の概念の拡張である──翻って,ベクトルはテンソルの特殊である。
「テンソル場」は,「ベクトル場」の「ベクトル」を「テンソル」にしただけのものである。
実際,「ベクトル場」を論じれば,「テンソル場」の論の骨格は尽くしたことになる。
そこで,「ベクトル場」から。
「ベクトル場」とは?
それは,空間の各点に量が立っている状態である。
量はベクトルであり,ゆえに「ベクトル場」である。
「空間の各点に量が立っている」とは,つぎのようなことである:
ここのいまの高さ
ここのいまの温度
ここのいまの重力
ここのいまの磁気
空間と量のこの対応を,記述しようとする。
記述の方法は,「座標」の導入である。
空間と量を,それぞれ \( \mathscr{S} \),\( \mathscr{V} \) で表す。
\( \mathscr{S} \) の場合は,原点をとり, 各点を位置ベクトルと見なす。
ベクトル空間 \( \mathscr{S} \) の次元をmとして,基底 \( E = (\, {\bf e}_1,\, \cdots \,,\, {\bf e}_m \,) \) をとる。
各 \( {\bf x} \in \mathscr{S} \) は,この基底に対し座標 \( (\, x_1,\, \cdots \,,\, x_m \,) \) をもつ。
\( \mathscr{V} \) の場合は,既にベクトル空間である。
次元をnとして,基底 \( F = (\, {\bf f}_1,\, \cdots \,,\, {\bf f}_n \,) \) をとる。
各 \( {\bf y} \in \mathscr{V} \) は,この基底に対し座標 \( (\, y_1,\, \cdots \,,\, y_n \,) \) をもつ。
「 基底 \( E = (\, {\bf e}_1,\, \cdots \,,\, {\bf e}_m \,) \) に対する \( {\bf x} \) の座標は \( (\, x_1,\, \cdots \,,\, x_m \,) \) 」
「 基底 \( F = (\, {\bf f}_1,\, \cdots \,,\, {\bf f}_n \,) \) に対する \( {\bf y} \) の座標は \( (\, y_1,\, \cdots \,,\, y_m \,) \) 」は,つぎの形に表現される:
\[
{\bf x} = x_1\,{\bf e}_1 + \cdots + x_m\,{\bf e}_m \\
{\bf y} = y_1\,{\bf f}_1 + \cdots + y_n\,{\bf f}_n
\]
しかし,ここでの「+」の記号的機能は,「互いを足す」ではなく「互いを分ける」である。
そこで,基底を取ることを,次元の数だけ1次元ベクトル空間に分解することだと考える。
係数体をKで表すと,その1次元ベクトル空間は,基底 \( {\bf e}_i \) に対し \( K{\bf e}_i \),基底 \( {\bf f}_k \) に対し \( K{\bf f}_k \) と書ける。
「分解」の記号は,「\( \otimes \) 」になる:
\[
\mathscr{S} = (K {\bf e}_1) \otimes \cdots \otimes (K {\bf e}_m) \\
\mathscr{V} = (K {\bf f}_1) \otimes \cdots \otimes (K {\bf f}_n) \\
\]
\( \mathscr{S} \) の要素 (空間の点) には \( \mathscr{V} \) の要素 (量) が対応している。
この対応を \( \Psi \) で表す:
\[
\Psi : \mathscr{S} \longrightarrow \mathscr{V}
\]
\( \Psi \) は,\( \mathscr{S},\, \mathscr{V} \) それぞれにおける基底の導入により,つぎの関数になる:
\[
\Psi_{EF} : (K {\bf e}_1) \otimes \cdots \otimes (K {\bf e}_m) \longrightarrow (K {\bf f}_1) \otimes \cdots \otimes (K {\bf f}_n)
\]
\( \Psi_{EF} \) は,座標間の対応を導く:
\[
\psi_{EF} : \overbrace{K \times \cdots \times K}^m \longrightarrow \overbrace{K \times \cdots \times K}^n
\]
このとき,Kが何の係数体なのかわからなくなる。
そこで,区別できるように添字をつけるとなる。
どうせつけるならはっきりわかるのがよい。
\( {\bf e}_i \) に対応するKは \( K^{{\bf e}_i} \) で表し,\( {\bf f}_k \) に対応するKは \( K^{{\bf f}_k} \) で表すことにする。
一般論にするために係数体Kも伏せようとするなら, \( T^{{\bf e}_i}, T^{{\bf f}_k} \) で表す。
「T」の文字は「Tensor」の「T」である。
こうして,\( \Psi_{EF} \) はつぎのようになる:
\[
\psi_{EF} : T^{{\bf e}_1} \times \cdots \times T^{{\bf e}_m} \longrightarrow T^{{\bf f}_1} \times \cdots \times T^{{\bf f}_n}
\]
\( \psi_{EF} \) からは,さらにつぎの n 個の関数が導かれる:
\[
{\psi_{EF}}_{(k)} : T^{{\bf e}_1} \times \cdots \times T^{{\bf e}_m} \longrightarrow T^{{\bf f}_k} \ \ \ \ \ (\, k = 1, \cdots , n \,)
\]
以上,場面と枠組の設定である。
そして,つぎの可換図式ができている:
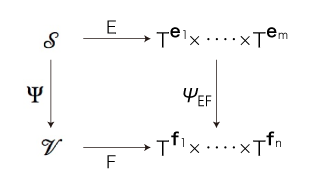
本題はここからになる。
関数 \( \psi_{EF} : T^{{\bf e}_1} \times \cdots \times T^{{\bf e}_m} \longrightarrow T^{{\bf f}_1} \times \cdots \times T^{{\bf f}_n} \) は,
(1) 変数であるところの \( T^{{\bf e}_1} \times \cdots \times T^{{\bf e}_m} \) の要素
(2) 定数
が組み合わさった計算式になるとする。
ここで,この計算式は「公式」に昇格できるか?と考える。
「公式」の意味は,「基底に依らない」である:
| |
\( \mathscr{S} \) の基底 \( E = (\, {\bf e}_1,\, \cdots \,,\, {\bf e}_m \,) \) を \( E^{'} = (\, {\bf e^{'}}_1,\, \cdots \,,\, {\bf e^{'}}_m \,) \) に換える。
この基底変換の表現行列を \( A \) とする:
\[
(\, {\bf e^{'}}_1,\, \cdots \,,\, {\bf e^{'}}_m \,) = (\, {\bf e}_1,\, \cdots \,,\, {\bf e}_m \,)\, A
\]
──このとき,\( A \)の逆行列 \( B = \left( {b^i}_j \right) \) はつぎの座標変換行列になる:
\[
\ \ \ \ \ \ \ \left( \begin{array}{c} {x^{'}}^1 \\ \vdots \\ {x^{'}}^m \\ \end{array} \right)
= \left(
\begin{array}{ccc}
{b^1}_1 & \cdots & {b^1}_m \\
& \cdots & \\
{b^m}_1 & \cdots & {b^m}_m \\
\end{array}
\right)
= \left( \begin{array}{c} x^1 \\ \vdots \\ x^m \\ \end{array} \right)
\]
\( \mathscr{V} \) の基底 \( F = (\, {\bf f}_1,\, \cdots \,,\, {\bf f}_n \,) \) を \( F^{'} = (\, {\bf f^{'}}_1,\, \cdots \,,\, {\bf f^{'}}_n \,) \) に換える。
この基底変換の表現行列を \( P \) とする:
\[
(\, {\bf f^{'}}_1,\, \cdots \,,\, {\bf f^{'}}_n \,) = (\, {\bf f}_1,\, \cdots \,,\, {\bf f}_n \,)\, P
\]
──このとき,\( P \) の逆行列 \( Q = \left( {q^k}_l \right) \) はつぎの座標変換行列になる:
\[
\ \ \ \ \ \ \ \left( \begin{array}{c} {y^{'}}^1 \\ \vdots \\ {y^{'}}^n \\ \end{array} \right)
= \left(
\begin{array}{ccc}
{q^1}_1 & \cdots & {q^1}_n \\
& \cdots & \\
{q^n}_1 & \cdots & {q^n}_n \\
\end{array}
\right)
= \left( \begin{array}{c} y^1 \\ \vdots \\ y^n \\ \end{array} \right)
\]
このとき,つぎの図式は可換:
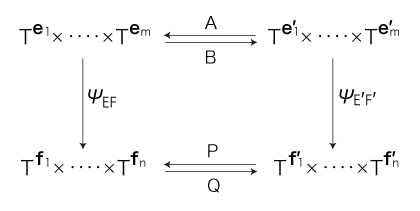
|
|
実際,この条件が満たされるとき,\( \psi_{EF} \) の生の定数を定数記号に置き換えて,「公式」が成る。
《形式を普遍とし,定数記号の値を座標系に依存させる》というわけである。
「公式」にまで行ったところで,「\( \mathscr{S} \) は \( \mathscr{V} \) ベクトル場である」となる。
ベクトル場に対しては,何を調べるのか。
位置の変化に対する量の変化の様子である:
<ここ・いま>の連続変化に対する,高さの変化は如何?
<ここ・いま>の連続変化に対する,温度の変化は如何?
<ここ・いま>の連続変化に対する,重力の変化は如何?
<ここ・いま>の連続変化に対する,磁気の変化は如何?
即ち,「解析」を課題にしていく
|

