「タテ×ヨコ×タカサ=体積」のテンソルは,「タテ×ヨコ=面積」のテンソルをやった後は,特段取り上げずともよいものである。
ただ,項が一つ増えることで記述がどのように増えるかは,見ておく方がよい。
ということで,「タテ×ヨコ×タカサ=体積」も,一応きちんと押さえておく。
「タテ×ヨコ×タカサ=体積」に対しては,つぎの構成要素を見る:
- 実ベクトル空間 \( U_1,\, U_2,\, U_3\)
\( U_1\) : タテ(長さ) 全体
\( U_2\) : ヨコ(長さ) 全体
\( U_3\) : タカサ(長さ) 全体
\( W \) : 体積全体
- 複線型写像 \( \phi : U_1 \times U_2 \times U_3 \to W\)
\( \phi \) : (タテ \({\bf x_1}\), ヨコ \({\bf x_2}\), タカサ \({\bf x_3}) \)
\( \qquad \longmapsto\) タテ \({\bf x}_1\), ヨコ \({\bf x}_2 \) タカサ \({\bf x}_3\) の直方体の体積
ここで,量をベクトル──大きさと向き──に見る方法は,量に「増」をつける:
「複線型写像 \( \phi : U_1 \times U_2 \times U_3 \to W\) 」の意味は:
- \(U_2\) の元 \({\bf u}_2\) と \(U_3\) の元 \({\bf u}_3\) を固定したときの写像
\( {\bf x}_1 \longmapsto \phi({\bf x}_1,\,{\bf u}_2,\,{\bf u}_3) \quad ({\bf x}_3 \in U_1) \)
は,\(U_3\) から \(W\) への線型写像
- \(U_3\) の元 \({\bf u}_3\) と \(U_1\) の元 \({\bf u}_1\) を固定したときの写像
\( {\bf x}_2 \longmapsto \phi({\bf u}_1,\,{\bf x}_2,\,{\bf u}_3) \quad ({\bf x}_1 \in U_2) \)
は,\(U_3\) から \(W\) への線型写像
- \(U_1\) の元 \({\bf u}_1\) と \(U_2\) の元 \({\bf u}_2\) を固定したときの写像
\( {\bf x}_3 \longmapsto \phi({\bf u}_1,\,{\bf u}_2,\,{\bf x}_3) \quad ({\bf x}_3 \in U_3) \)
は,\(U_3\) から \(W\) への線型写像
実際,小学数学では,つぎのことが指導される:
「タテの長さが2倍,3倍,‥‥ になれば,
直方体の体積も2倍,3倍,‥‥ になる。
ヨコ,タカサについても同様。」
つぎは,集合 \(U_1 \times U_2 \times U_3\) 上の同値関係になる:
\[
({\bf x}_1,\,{\bf x}_2,\,{\bf x}_3) \sim ({\bf x’}_1,\,{\bf x'}_2,\,{\bf x'}_3)
\\ \qquad \ :\
\phi({\bf x}_1,\,{\bf x}_2,\,{\bf x}_3) = \phi({\bf x}_1,\,{\bf x}_2,\,{\bf x}_3)
\]
この同値関係による \(U_1 \times U_2 \times U_3\) の商集合──同値類の集合──を「\(U_1 \bigotimes U_2 \bigotimes U_3\)」で表す。
また,\( ({\bf x}_1,\,{\bf x}_2,\,{\bf x}_3)\) が代表元になる同値類を,「\({\bf x}_1 \otimes {\bf x}_2 \otimes {\bf x}_3\)」で表す。
「\(U_1 \otimes U_2 \otimes U_3\)」は,即ち「タテ\(\bigotimes\)ヨコ\(\bigotimes\)タカサ」である。
ここでは,直方体の体積が同じになる (タテ, ヨコ, タカサ) を類別したわけである。
\(U_1 \otimes U_2 \otimes U_3\) は,つぎの算法を以て,実ベクトル空間になる:
\[
\begin{align*}
\xi\,({\bf x}_1 \otimes {\bf x}_2 \otimes {\bf x}_3)
&= (\xi\,{\bf x}_1) \otimes {\bf x}_2 \otimes {\bf x}_3
\\&= {\bf x}_1 \otimes (\xi\,{\bf x}_2) \otimes {\bf x}_3
\\&= {\bf x}_1 \otimes {\bf x}_2 \otimes ( \xi\,{\bf x}_3)
\quad ( \xi \in \mathbb{R} )
\end{align*}
\]
\[
{\bf x}_1 \otimes {\bf x}_2 \otimes {\bf x}_3 + {\bf x'}_1 \otimes {\bf x}_2 \otimes {\bf x}_3
= ({\bf x}_1 + {\bf x'}_1 ) \otimes {\bf x}_2 \otimes {\bf x}_3
\\
{\bf x}_1 \otimes {\bf x}_2 \otimes {\bf x}_3 + {\bf x}_1 \otimes {\bf x'}_2 \otimes {\bf x}_3
= {\bf x}_1 \otimes ({\bf x}_2 + {\bf x'}_2) \otimes {\bf x}_3
\\
{\bf x}_1 \otimes {\bf x}_2 \otimes {\bf x}_3 + {\bf x}_1 \otimes {\bf x}_2 \otimes {\bf x'}_3
= {\bf x}_1 ) \otimes {\bf x}_2 \otimes ({\bf x}_3 + {\bf x'}_3)
\]
また,写像:
\[
U_1 \times U_2 \times U_3 \longrightarrow U_1 \otimes U_2 \otimes U_3
\\
\ ({\bf x}_1,\,{\bf x}_2,\,{\bf x}_3) \longmapsto {\bf x}_1 \otimes {\bf x}_2 \otimes {\bf x}_3
\]
は,員にそれが属するクラスを対応させる写像──「標準写像 canonical map」──である。
そして,つぎの図式を可換にする写像 \(\bar{\phi} \) は,線型空間 \(U_1 \bigotimes U_2 \bigotimes U_3\) と \( W\) の同型写像になる:
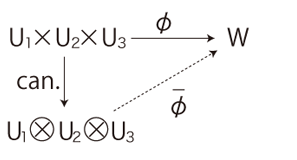
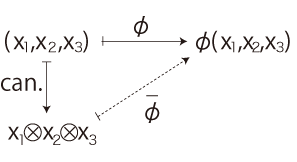
この同型が,「タテ × ヨコ × タカサ = 体積」と読まれる。
同型「タテ\(\bigotimes\)ヨコ\(\bigotimes\)タカサ \( \approx \) 体積」の読みが「タテ × ヨコ × タカサ = 体積」というわけである。
|

