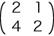線型変換f: E → E による E の像 Im(f) がどうなるかを,ここで問題にする。
Im(f) がどうなるかを観察すると,つぎのことがわかる (実際,これは確かめられる):
Im(f) は,原点を通る超平面 (部分線型空間) である。
ここで,つぎの2つを区別する:
- Eの次元が減少 (もとの空間が潰れる)
- Eの次元を保持 (潰れない)
Aを「退化」と呼び,Bを「非退化」と呼ぶ。
Eの次元を n とするとき,退化にはつぎの場合がある:
1次元減少
2次元減少
‥‥
nー2 次元減少 (原点を通る平面に潰れる)
nー1 次元減少 (原点を通る直線に潰れる)
n次元減少 (原点に潰れる)
以上の観察から,つぎの問題を立てたくなる:
- f がどんな場合,退化か? (fがどんな場合,非退化か?)
- 退化で減少する次元は,何によって決まるか?
この答えは,つぎのようになる:
- Eの基底 {u1, u2, ‥‥, un } に対し,f(u1), f(u2), ‥‥, f(un) が互いに1次独立なら,非退化。
- 互いに1次従属なものが k+1 個なら,k次元減少の退化。
また,f の表現行列Aを使えば,つぎのように言い直すことができる:
- Aの行が互いに1次独立なら,非退化。
- 互いに1次従属なものが k+1 個なら,k次元減少の退化。
ここで,Ker(f) の概念を,つぎの定義によって導入する:
Ker(f) は原点を通る超平面 (部分線型空間) になることが確かめられる。
また,「非退化」が,Ker(f) を使ってつぎのように特徴づけられるようになる:
Ker(f) = {0} (0次元) が,非退化の条件になる
| 確認 : |
退化とは,基底 {u1, u2, ‥‥, un } に対し,f(u1), f(u2), ‥‥, f(un) が互いに1次従属であること。
すなわち,すべてが0ではない α1, α2, ‥‥, αn で,
f(u1) × α1
+ f(u2) × α2
+ ‥‥
+ f(un) × αn = 0
となるものがとれること。
そしてこの相等関係は,つぎのことと同じ:
a= u1 × α1
+ u2 × α2
+ ‥‥
+ un × αn
f(a) = 0
|
よって,「0 と異なるEの要素で Ker(f) に属するものが存在する」が,退化の条件。
言い換えると,Ker(f) = {0} が,非退化の条件。
|
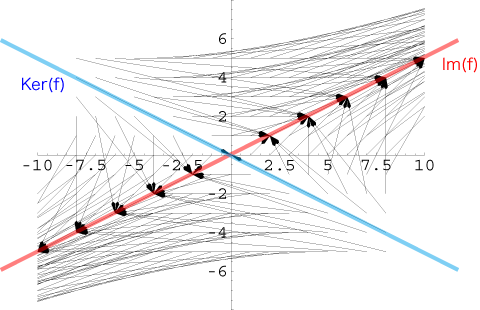
Im(f),Ker(f) のイメージをもつために,表現行列が
の線型変換 f および Im(f),Ker(f) を作図してみる:
この図を観察すると,つぎのように見えてくる:
| Ker(f) | : | 全空間Eを潰すのに使う超平面 |
| Im(f) | : | 全空間Eを潰した先の超平面 |
さらに,3次元の場合で,このイメージを試されたい:
- 全空間を原点を通る平面に潰す場合 (Ker(f) が1次元で Im(f) が2次元)
- 全空間を原点を通る直線に潰す場合 (Ker(f) が2次元で Im(f) が1次元)
- 全空間を原点に潰す場合 (Ker(f) が3次元で Im(f) が0次元)
このイメージは,Ker(f) の次元と Im(f) の次元の和が Eの次元に等しいことを示唆している (実際,このことは確かめられる):
dim( Ker(f) ) + dim( Im(f) ) = dim( E )
|