一方,小数の商の式に対応する小数が存在するとは限らない。 そこでいま,1.25 × 4.8 = 6 を転じた 6 ÷ 1.25 の式で,「小数のわり算」の推論を見ることにする。 これは,以下のようになる: 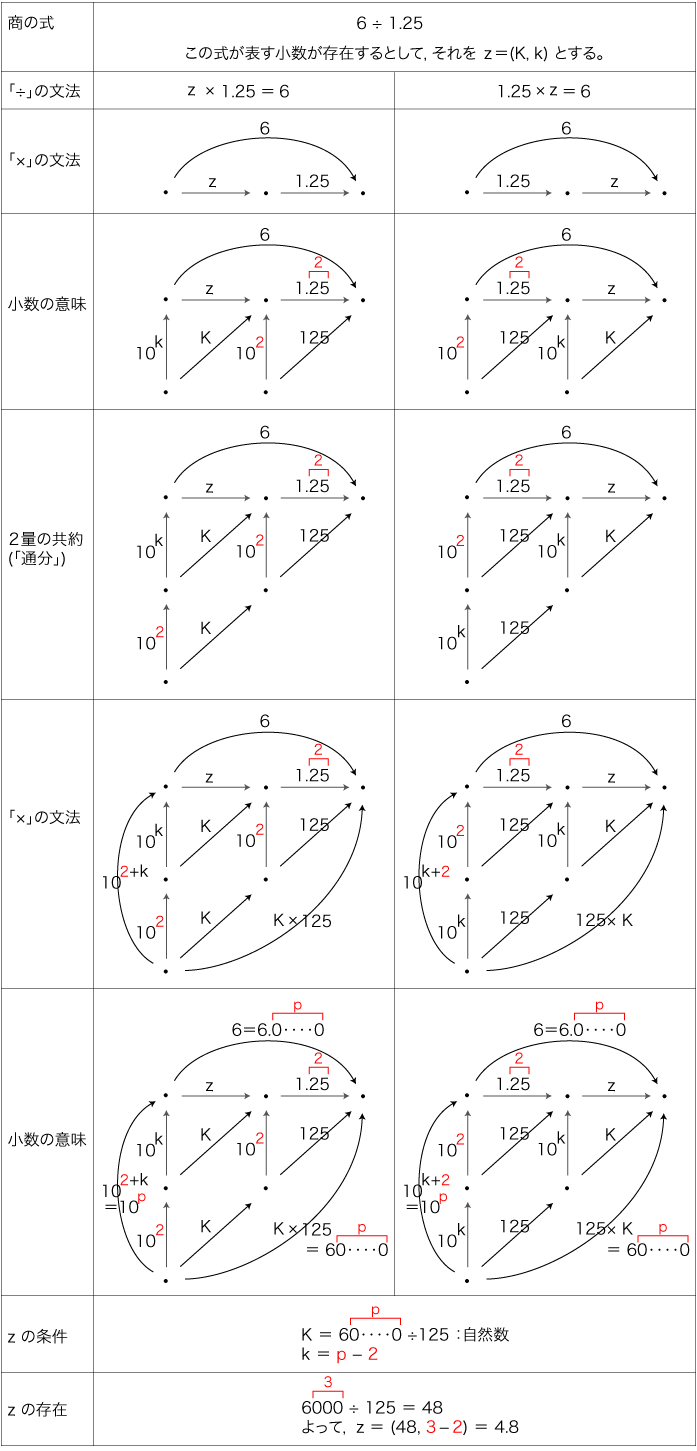
さらに,0追加の過程を見直すことで,学校で指導されているつぎの「小数のわり算」に至る: 例:6 ÷ 1.25 |
| Up | 小数の商,求商法 | 作成: 2012-02-13 更新: 2012-02-15 |
一方,小数の商の式に対応する小数が存在するとは限らない。 そこでいま,1.25 × 4.8 = 6 を転じた 6 ÷ 1.25 の式で,「小数のわり算」の推論を見ることにする。 これは,以下のようになる: 
さらに,0追加の過程を見直すことで,学校で指導されているつぎの「小数のわり算」に至る: 例:6 ÷ 1.25 |