数学では,集合に構造を導入したものを,空間と呼ぶ。 空間に対しては,「部分空間」の概念が導入される。 「部分」の意味は,「集合の部分であって,空間の構造に関してそれ自体閉じている」である。 例えば,環Aに対して「Aの部分環」が考えられる。 これの意味は,「Aの部分集合であって,Aの環構造を定義している二つの算法──加法と乗法──に関して閉じているもの」である。 分数全体の集合は,乗法と加法の二つの算法で定義される構造をもつ空間になる。 小数全体の集合も,乗法と加法の二つの算法で定義される構造をもつ空間になる。 いま,「小数倍を分数倍に解釈」をやるときの小数と分数の対応で以て,小数の集合を分数の集合に埋め込む。 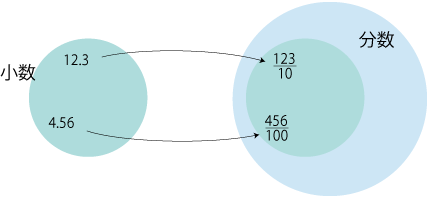
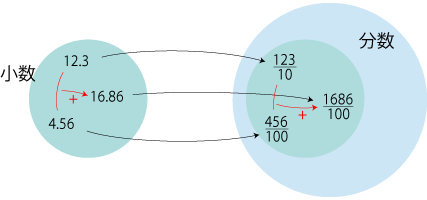
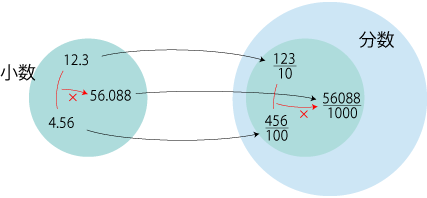
要点: 小数を分数 (「有理数」) と見なせるのは, |