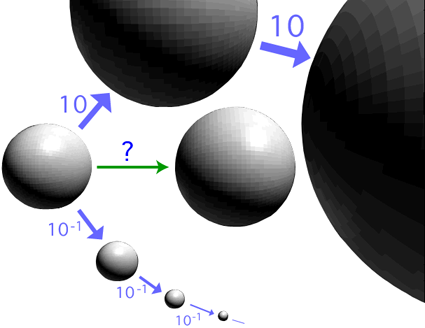
10個の10個が2つ 10個が3つ 個が1つ と同じになる。 このことを転じて,
10個の10個の10個 10個の10個 10個 個 の単位システム── 十進の単位システム──を予めつくっておいて,
10個の10個の10個がいくつ(3) 10個の10個がいくつ(2) 10個がいくつ(1) 個がいくつ(0) (「いくつ(k)」は 0〜9) と数える。 このとき,
が個数と一致する。 「1, 2, 3, ‥‥」と一つずつ数えていくやり方と比べると,この方法は計数の労力を劇的に減らすものになっている。 これが,計数における十進数のメリットである。
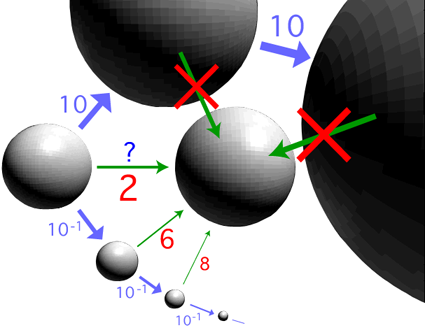
ここで,場面は「順序稠密量」になる。 順序稠密量が対象化され,順序稠密量の表現が課題とされる。 離散量は,「個」という原子(部分のないもの)を考える。 この「部分がない」の制約を外して「任意に部分をとれる」にすると,順序稠密量の概念になる。 順序稠密量の「稠密」の意味は,「任意に部分をとれる」である。 離散量では,量を「個がいくつ」で表した。 このことを,ここでつぎのように解釈する:
順序稠密量を表現するのに,十進数による個数の数え方を素直に拡張 (延長) する。 すなわち,単位からつぎの単位システムを導く:
単位の10倍の10倍の10倍 単位の10倍の10倍 単位の10倍 単位 単位の10−1倍 単位の10−1倍の10−1倍 単位の10−1倍の10−1倍の10−1倍 ‥‥ そして,量をつぎのように測る:
単位の10倍の10倍の10倍がいくつ(3) 単位の10倍の10倍がいくつ(2) 単位の10倍がいくつ(1) 単位がいくつ(0) 単位の10−1倍がいくつ(−1) 単位の10−1倍の10−1倍がいくつ(−2) 単位の10−1倍の10−1倍の10−1倍がいくつ(−3) ‥‥ (「いくつ(k)」は 0〜9) そして,つぎを倍の表現にする:
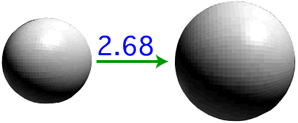
「.」は,どれが [いくつ(0)] かを示すための記号で,「小数点」と呼ぶ。 [いくつ] をただ並べただけでは,倍の表現が一意にならない。そこで,「小数点」のような工夫が必要になるわけである。 例:
この方法で表現された倍は,0〜9と小数点がつくる文字列になっている。 この文字列を「数」と定めて,「小数」と呼ぶ。 「数」と定める根拠は,これが倍の表現になっており,そして (この後で示されるように)「数の和・積」をこれに対して定義することができるからである。 小数による量表現は,十進数による個数表現とつぎのようにつながっている:
<単位の10−m倍>の [いくつ(n)] ‥‥ [いくつ(1)] [いくつ(0)] [いくつ(−1)] ‥‥ [いくつ(−m)] 倍。 実際,この関係を用いることで,小数の和・積の筆算法が導かれる。 すなわち,小数の和・積は,十進数の和・積の筆算と小数点の処理を合わせる形で,求められるものになる。 (  小数の算法) 小数の算法)
|