正方形の辺と対角線の長さの比 x は,代数的無理数の √2 です。
- x が √2 であること
ピタゴラスの定理 (三平方の定理) より,x2 = 12 + 12 = 2 が成り立つ。よって,x は √2 。
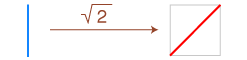
- √2 が無理数であること
これの証明は,つぎの2タイプが考えられます:
- 「√2 が有理数であるわけがない──有理数だったらおかしいことになる」を証明する。(背理法)
- √2 は,正方形の辺と対角線の長さの比。
この比をユークリッドの互除法で求めようとして,操作が永遠に続いて終わらないものなら,√2 は有理数ではない。
そこで,「この操作は永遠に続いて終わらない」を証明する。(直接法)
Aタイプ (背理法) の証明:
√2 が無理数でないとする──有理数 a/b (a, b は互いに素) であるとする。
(a/b)2 = 2 より,a2 = 2 × b2。よって,a は偶数。そこで,a = 2 × c とおくと,(2 × c)2 = 2 × b2,2 × c2 = b2,よって b は偶数。
これは,「a, b は互いに素」に矛盾。
よって, (背理法により) √2 は無理数でなければならない。
Bタイプ (直接法) の証明:
(わたしはこの証明を,1970代か1980年代の『数学セミナー』に載った森毅の論文を読んで,知りました。)
- 辺が対角線にいくつ入り,そしてそのときの余りは?
- 1つ入って,余りが出る:
- 余りは,もとの辺にいくつ入入り,そしてそのときの余りは?
- 余りと同じ長さの線分が,つぎのようにとれる:
- つぎのようにして,2つ入って,余りが出る:
- この余りは,もとの余りにいくつ入り,そしてそのときの余りは?
これは,3 と同じ形になっている。
よって,この「ユークリッドの互除法」は永遠に続く。
|