3.2 順序構造を伴う数の系
学校数学では,複素数(ないし四元数)を除いて,数の系に対しては順序構造を導入することになる。この順序構造を伴う数の系は,以下のように定式化される。
数の系 (N,+,×) とこれの上の全順序関係≦に対し,N+を,
- Nが+に関して群であるときはNの正元(≧0の元)全体,
- そうでないときはN自身
とし,N*+=N*∩N+とする(この記号法は本論文全体を通じて用いる)。
系 (N,+,×,≦) において以下の条件が満たされるとき,これを順序構造を伴う数の系と呼ぶ:
- ζ∈N*+に対し
ξ<ξ+ζ
また,+が群算法のとき,ζ<0に対し
ξ+ζ<ξ
- ξ,η∈N+,ζ∈N*+に対し,
ξ<η
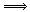 ξ×ζ<η×ζ
ξ×ζ<η×ζ
順序構造を伴う数の系においては,以下のことが成り立つ:
- +が群算法のとき,
ξ<0
 −ξ>0(註1)
−ξ>0(註1)
ξ≦η 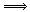 ξ+ζ≦η+ζ ξ+ζ≦η+ζ
|
| あるいは,同じこととして(註2),
|
ξ<η 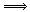 ξ+ζ<η+ζ(註3) ξ+ζ<η+ζ(註3)
|
- ξ<ηであるためには,ξ+ζ=ηとなるζ∈N*+の存在することが必要十分(註4).
- 1∈N*+(註5)
- ×が群算法のとき,
ξ∈N+*
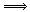 ξ-1∈N+*(註6)
ξ-1∈N+*(註6)
- N+,N*+は,×に関して閉じている──即ち,ξ,ηがN+[N*+]の要素ならばξ×ηもN+[N*+]の要素(註7).
- ζ∈N*+に対し,
ξ<η
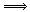 ξ×ζ<η×ζ(註8)
ξ×ζ<η×ζ(註8)
順序構造を伴う数の系は,+に関して群であれば,定義から,順序群である。この場合,N+に対し,N-で負元(≦0の元)全体の集合(={−ξ|ξ∈N+})を表わすことにする。
さらに,順序構造を伴う数の系は,体であれば順序体である。
(註1) ξ<0のとき,−ξ>(−ξ)+ξ=0。また,−ξ>0のとき,ξ<ξ+(−ξ)=0。
(註2) ξ≦ηからξ+ζ≦η+ζが導かれるとき,ξ<ηからもξ+ζ≦η+ζが導かれる。ξ+ζ=η+ζからは(数の系の定義より)ξ=ηが導かれるから,結局,ξ<ηからはξ+ζ<η+ζが導かれる。
逆に,ξ<ηからξ+ζ<η+ζが導かれるとき,明らかにξ≦ηからξ+ζ≦η+ζが導かれる。
(註3) ξ<ηとする。
(1) ξ+ρ=ηのとき:先ずρ∈N*。
(1-1) ρ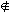 N+なら,+は群算法でρ<0,よって−ρ∈N+。そしてこのとき,ξ=ξ+η+(−η)=ξ+η+((−ξ)+(−ρ))=η+(−ρ)>ηとなり,仮定に反する。よってρ∈N+。
N+なら,+は群算法でρ<0,よって−ρ∈N+。そしてこのとき,ξ=ξ+η+(−η)=ξ+η+((−ξ)+(−ρ))=η+(−ρ)>ηとなり,仮定に反する。よってρ∈N+。
(1-2) ρ∈N+なら,ξ+ζ<ξ+ζ+ρ=η+ζ。
(2) ξ=η+ρのとき:先ずρ∈N*。ρ∈N+とすると,ξ=η+ρ>ηとなり,仮定に反する。よって,ρ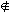 N+。そしてこのときには+が群算法でρ<0,さらに−ρ∈N+。そしてこのとき,ξ+ζ<ξ+ζ+(−ρ)=(η+ρ)+ζ+(−ρ)=η+ζ。
N+。そしてこのときには+が群算法でρ<0,さらに−ρ∈N+。そしてこのとき,ξ+ζ<ξ+ζ+(−ρ)=(η+ρ)+ζ+(−ρ)=η+ζ。
(註4) (1) ξ<ηとする。
(1-1) ξ+ζ=ηとする。このとき,先ずζ∈N*。もしζ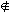 N+なら,+は群算法でζ<0,さらにη=ξ+ζ<ξとなり,仮定に反する。よってζ∈N+。
N+なら,+は群算法でζ<0,さらにη=ξ+ζ<ξとなり,仮定に反する。よってζ∈N+。
(1-2) ξ=η+ζとする。このとき,先ずζ∈N*。もしζ∈N+なら,η<η+ζ=ξとなり仮定に反する。よってζ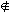 N+。そしてこのとき+は群算法でζ<0,よって−ζ∈N+。しかも,ξ+(−ζ)=(η+ζ)+(−ζ)=η。
N+。そしてこのとき+は群算法でζ<0,よって−ζ∈N+。しかも,ξ+(−ζ)=(η+ζ)+(−ζ)=η。
(2) ξ+ζ=ηかつζ∈N*+のとき,ξ<ξ+ζ=η。
(註5) もし1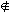 N*+なら,+は群算法で1<0。よって−1>0。しかしこのとき,−1=1×(−1)<0×(−1)=0となり,不合理。
N*+なら,+は群算法で1<0。よって−1>0。しかしこのとき,−1=1×(−1)<0×(−1)=0となり,不合理。
(註6) ξ∈N*+とする。もしξ-1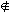 N*+ならば,+は群算法でξ-1<0。しかしこのとき,1=ξ-1×ξ<0×ξ=0となり,不合理。
N*+ならば,+は群算法でξ-1<0。しかしこのとき,1=ξ-1×ξ<0×ξ=0となり,不合理。
(註7) N+≠Nのとき+は群算法。そしてこのとき,0<ξかつη>0からは,0=0×η<ξ×ηが導かれる。
(註8) N+≠Nのとき+は群算法。このとき,ξ<ηかつζ>0とする。η+(−ξ)>ξ+(−ξ)=0が導かれる。N*+は×に関して閉じているから,η×ζ+(−(ξ×ζ))=η×ζ+(−ξ)×ζ=(η+(−ξ))×ζ>0。さらに,η×ζ=η×ζ+(−(ξ×ζ))+ξ×ζ>0+ξ×ζ=ξ×ζ。
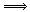 ξ×ζ<η×ζ
ξ×ζ<η×ζ
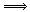 ξ×ζ<η×ζ
ξ×ζ<η×ζ
 −ξ>0(註1)
−ξ>0(註1)
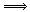 ξ+ζ≦η+ζ
ξ+ζ≦η+ζ
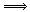 ξ+ζ<η+ζ(註3)
ξ+ζ<η+ζ(註3)
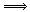 ξ-1∈N+*(註6)
ξ-1∈N+*(註6)
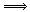 ξ×ζ<η×ζ(註8)
ξ×ζ<η×ζ(註8)
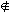 N+なら,+は群算法でρ<0,よって−ρ∈N+。そしてこのとき,ξ=ξ+η+(−η)=ξ+η+((−ξ)+(−ρ))=η+(−ρ)>ηとなり,仮定に反する。よってρ∈N+。
N+なら,+は群算法でρ<0,よって−ρ∈N+。そしてこのとき,ξ=ξ+η+(−η)=ξ+η+((−ξ)+(−ρ))=η+(−ρ)>ηとなり,仮定に反する。よってρ∈N+。
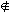 N+。そしてこのときには+が群算法でρ<0,さらに−ρ∈N+。そしてこのとき,ξ+ζ<ξ+ζ+(−ρ)=(η+ρ)+ζ+(−ρ)=η+ζ。
N+。そしてこのときには+が群算法でρ<0,さらに−ρ∈N+。そしてこのとき,ξ+ζ<ξ+ζ+(−ρ)=(η+ρ)+ζ+(−ρ)=η+ζ。
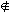 N+なら,+は群算法でζ<0,さらにη=ξ+ζ<ξとなり,仮定に反する。よってζ∈N+。
N+なら,+は群算法でζ<0,さらにη=ξ+ζ<ξとなり,仮定に反する。よってζ∈N+。
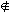 N+。そしてこのとき+は群算法でζ<0,よって−ζ∈N+。しかも,ξ+(−ζ)=(η+ζ)+(−ζ)=η。
N+。そしてこのとき+は群算法でζ<0,よって−ζ∈N+。しかも,ξ+(−ζ)=(η+ζ)+(−ζ)=η。
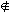 N*+なら,+は群算法で1<0。よって−1>0。しかしこのとき,−1=1×(−1)<0×(−1)=0となり,不合理。
N*+なら,+は群算法で1<0。よって−1>0。しかしこのとき,−1=1×(−1)<0×(−1)=0となり,不合理。
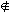 N*+ならば,+は群算法でξ-1<0。しかしこのとき,1=ξ-1×ξ<0×ξ=0となり,不合理。
N*+ならば,+は群算法でξ-1<0。しかしこのとき,1=ξ-1×ξ<0×ξ=0となり,不合理。